Introduction
In this article we are going to see what a quadratic function is, its mathematical expression, its characteristics, how to graph it in the Cartesian plane and what it can be useful for in the development of games with examples in Unity.
Mathematical expression of a quadratic function
The polynomial expression of a quadratic function is:

It is commonly read “f of x”, being X the independent variable, a, b and c constant real numbers.
Characteristics of a quadratic function
Domain
The domain is the range of allowable values for the independent variable, commonly referred to as X.
In the case of the quadratic function the domain is the set of real numbers.
In other words we can choose any value of X belonging to the set of real numbers and we will find its corresponding value f (X).
Click here to read the article on number sets.
Graph in Cartesian plane of a quadratic function
The graph of f (X) in the Cartesian plane is a parabola.
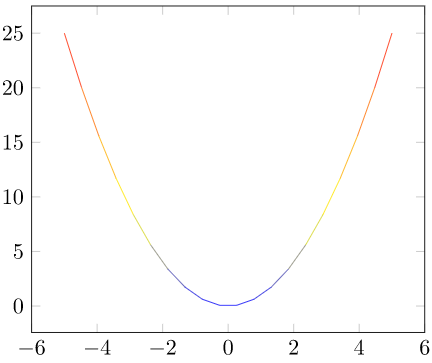
Fig. 1: Graph of a quadratic function with positive “a” coefficient.

Fig. 1: Graph of a quadratic function with negative “a” coefficient.
If you are interested you can read more about the Cartesian system in this article.
Function Roots
The roots of a quadratic function are the values of x for which f (x) is worth 0, i.e. the points at which the function touches the abscissa axis (commonly the x-axis).
There can be three cases, the function has a root, i.e. there is only one value of x for which the function is worth 0.
The function can have two roots, i.e. there are two different values of x for which the function is worth 0.
The function may not have roots in the set of real numbers but in the set of complex numbers.
To calculate the roots of a quadratic function we use a formula commonly known as the Bhaskara formula.
Given the following equation:

The two values of x that satisfy this equation are given by:

The plus-minus sign ( ± ) means that they are two equations, in one we use the plus sign and get X1 and in another we use the minus sign and get X2.
As an observation, if what is inside the square root gives as a result a negative number it means that the equation has no solution in the set of real ones, in this case we see graphically that the parabola does not cut the axis of the abscissas.
Some examples in Unity of quadratic function
Draw parabolic trajectories
We might be interested in drawing parabolic trajectories through code, for example for particle systems, or to represent the possible trajectory a projectile can follow when launching it.
In the following video I show how a set of GameObjects follow a parabolic path described by two quadratic functions to which the parameters can be adjusted.
Observation 1: spheres of the same color follow the path defined by the same equation only that for one I take the constant a as positive and in the other as negative, for this reason they are reflected with respect to the axes.
Note 2: Notice that at the beginning and end of the video the value of a is 0, this means that the quadratic term is annulled and we are left with a linear function.
Implement quadratic magnitudes
In physics there are many quadratic magnitudes that we might be interested in implementing in our game.
An example of this can be motion with constant acceleration, i.e. objects that move with velocity that changes linearly. For example, bodies in free fall by the action of gravity or vehicles that accelerate.
Some types of energy such as kinetic energy or elastic potential energy are proportional to the square of a magnitude.
Conclusion
The quadratic function is a polynomial function of order 2 whose graph in the Cartesian plane is a parabola.
The roots of the quadratic function are the values of x in which f (x) = 0 is fulfilled. We can use Bhaskara’s formula to find them.
A quadratic function can have two different roots, a root or not have roots in the set of real numbers. If a quadratic function does not have real roots, it does not graphically intersect the abscissa axis.
There are physical magnitudes as well as trajectories of accelerated bodies that can be described by quadratic functions, so it is useful to have knowledge about their characteristics and thus be able to implement them correctly in Unity.
