Introduction

In this arti­cle we are going to see what a lin­ear func­tion is, its math­e­mat­i­cal expres­sion, its char­ac­ter­is­tics, how to graph it in the Carte­sian plane and what it can be use­ful for in the devel­op­ment of videogames with exam­ples in Unity.

Mathematical expression of a linear function

A lin­ear func­tion is a poly­no­mi­al func­tion whose expres­sion is:

f (X) = a . X + b

It is com­mon­ly read "f of x", being X the inde­pen­dent vari­able, a and b con­stant real numbers.

Ana­lyz­ing the expres­sion we see that giv­en any val­ue of X, we first mul­ti­ply it by a and then add b. The result of all that oper­a­tion will be the val­ue of f (X).

Characteristics of a linear function 

Domain

The domain is the range of allow­able val­ues for the inde­pen­dent vari­able, com­mon­ly referred to as X.

In the case of the lin­ear func­tion, the domain is the set of real numbers.

In oth­er words we can choose any val­ue of X belong­ing to the set of real num­bers and we will find its cor­re­spond­ing val­ue f (X).

Graph in the Cartesian plane of a linear function

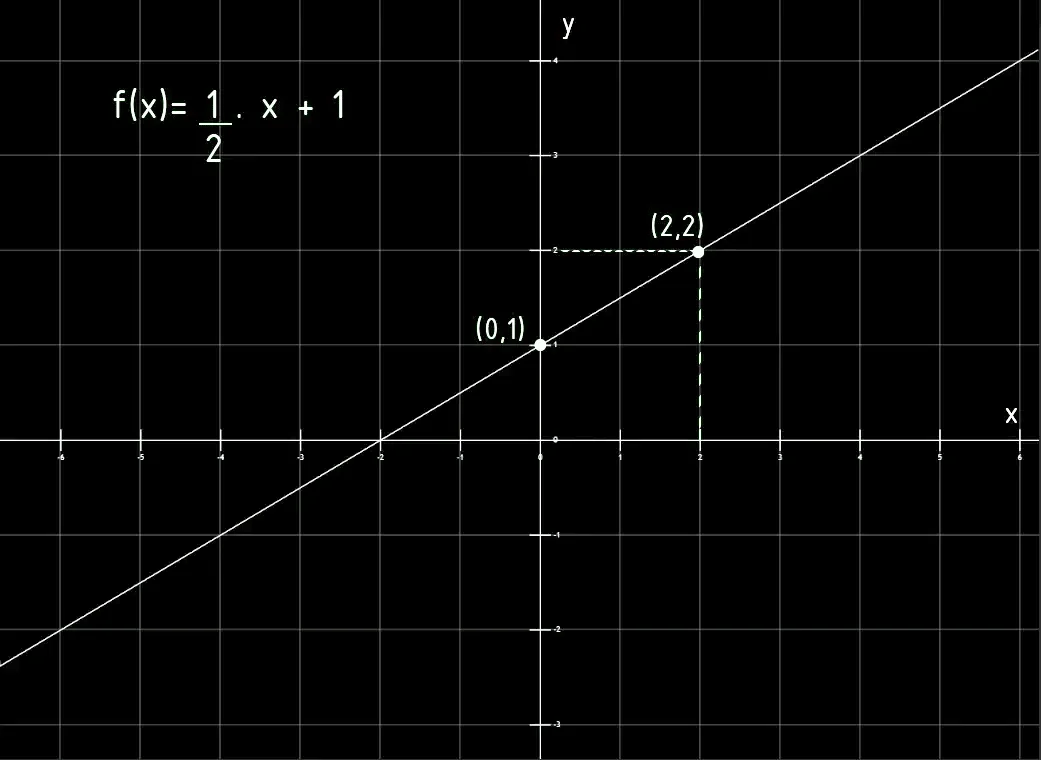
The graph of f (X) in the Carte­sian plane is a straight line. We can eas­i­ly draw it by find­ing two points of the func­tion and then using a ruler, draw the line that joins the two points.

We can eas­i­ly find one of these points by con­sid­er­ing X = 0.

The sec­ond point can be found by choos­ing a dif­fer­ent val­ue for X and mak­ing cal­cu­la­tions, for exam­ple for the func­tion in fig­ure 1, if we con­sid­er X = 2, the result of f (X) is equal to 2.

Ordinate of the origin

It is the val­ue of the func­tion when X = 0, graph­i­cal­ly it is the point where the func­tion cuts off the ver­ti­cal axis known as the ordi­nate axis. This point is known as the ordi­nate to the ori­gin.

In the graph of fig­ure 1 we see that the ordi­nate to the ori­gin is the point (0,1).

Abscissa of the origin

Anal­o­gous­ly to the pre­vi­ous case, the abscis­sa of the ori­gin is the point at which the func­tion inter­sects the hor­i­zon­tal axis or abscis­sa axis. At this point Y = 0.

A lin­ear func­tion may have no abscis­sa at the ori­gin if it is a line par­al­lel to the x‑axis and displaced.

In the graph of fig­ure 1 we see that the abscis­sa of the ori­gin is the point (-2,0).

Slope of a linear function

The term that mul­ti­plies X is known as slope and is the one that estab­lish­es how much the func­tion changes when the vari­able X changes by one unit. 

If we only have the graph of a lin­ear func­tion, we can cal­cu­late the slope as the tan­gent of the angle that forms the line with the hor­i­zon­tal axis. We can also find the slope using the Pythagore­an Theorem.

Parallel lines

Two straight lines are par­al­lel if they have the same slope.

Exam­ple of two par­al­lel lines: 

f (X) = 2 . X — 1 

g (X) = 2 . X + 3 

Perpendicular lines

Two straight lines are per­pen­dic­u­lar if the slope of one of them is equal to invert­ing the slope of the oth­er and mul­ti­ply­ing it by ‑1.

Exam­ple of two per­pen­dic­u­lar lines:

f (X) = 3 . X + 2 

g (X) = — ( 1/3 ) . X + 5 

Some examples in Unity of linear function

The lin­ear func­tion is one of the most use­ful math­e­mat­i­cal func­tions and its field of appli­ca­tion is very var­ied. Let's give some exam­ples of pos­si­ble applications.

Represent trajectories

The most basic thing I can think of is for objects to move in a straight path, which can be described as a lin­ear function.

For exam­ple in fig­ure 2 we see a scene in Uni­ty in which the spheres are describ­ing a tra­jec­to­ry that is described as their posi­tion in x is equal to their posi­tion in y.

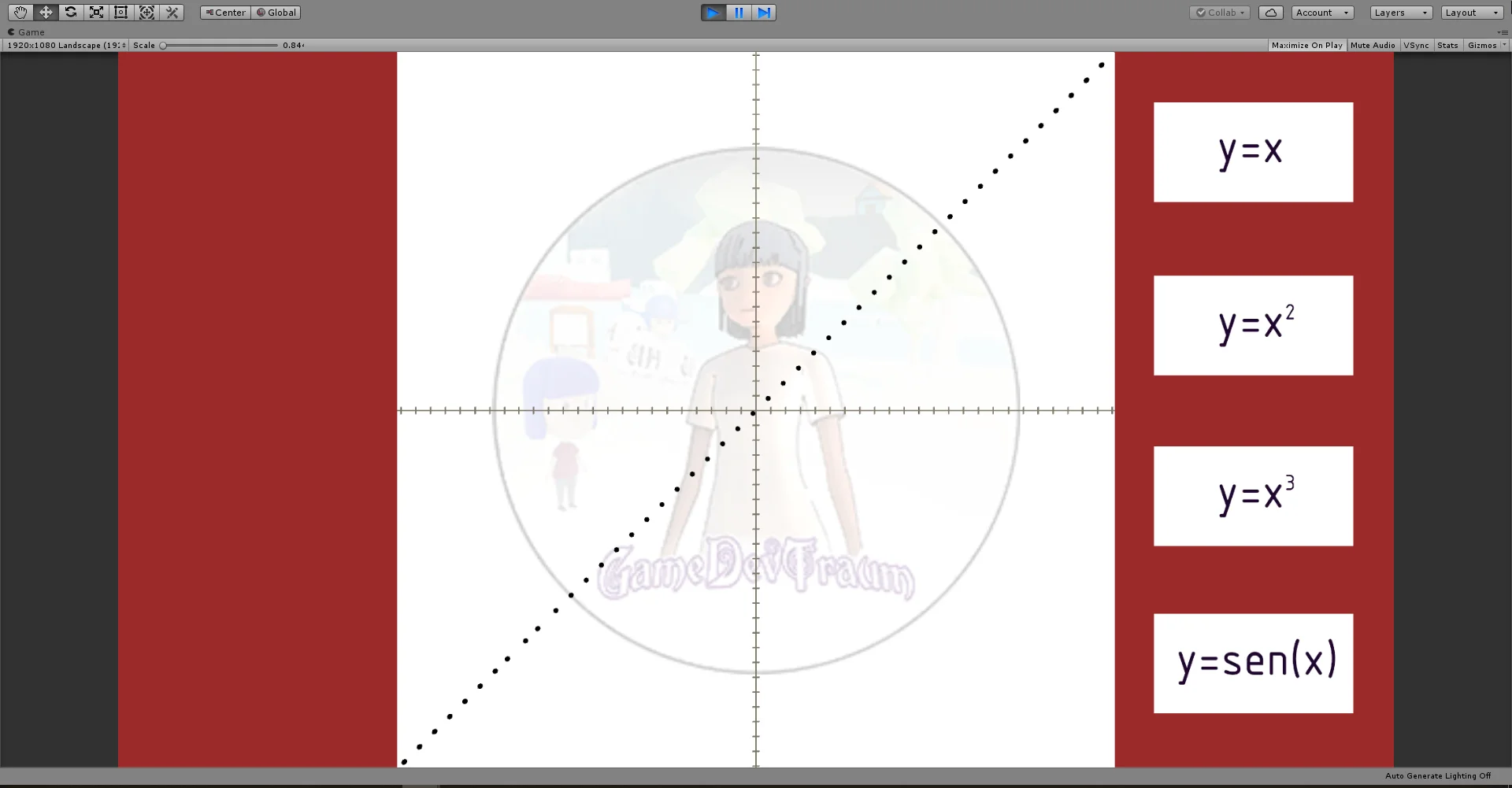
The same con­cept and with dif­fer­ent com­bi­na­tions of planes can be applied to oth­er cas­es such as vehi­cle move­ments, pro­jec­tile tra­jec­to­ries, etc.

In the last video of my Uni­ty fun­da­men­tal series, I use a lin­ear func­tion for the move­ment of the cam­era, which advances inside the tunnel.

Relate parameters linearly

Let's sup­pose that we have any two para­me­ters, for exam­ple the posi­tion of the play­er on the X axis and the rota­tion of a mech­a­nism with respect to one of its axes.

Let's also say that we would like these para­me­ters to be con­nect­ed in some way, that is to say that the rota­tion of the mech­a­nism will depend on the posi­tion of the player. 

We can then estab­lish a lin­ear rela­tion­ship between these two para­me­ters, for exam­ple we could say that the rota­tion of the mech­a­nism with respect to its z‑axis is equal to half the val­ue of the player's posi­tion on the x‑axis plus five units.

With this we can relate these two para­me­ters through a lin­ear function.

Implement linear magnitudes in our game

In physics there are many lin­ear mag­ni­tudes that we might be inter­est­ed in imple­ment­ing in our game. An exam­ple of this can be the uni­form rec­ti­lin­ear move­ment, in which we have a direc­tion of move­ment estab­lished and the posi­tion will be defined by a lin­ear func­tion in which the slope of the line is the veloc­i­ty of the object and the ordi­nate to the ori­gin is the ini­tial position.

In the case of Ohm's Law for exam­ple, if we have a cir­cuit with a source con­nect­ed to a resis­tance, the cir­cu­lat­ing cur­rent is equal to the volt­age of the source divid­ed the resis­tance, this is noth­ing oth­er than a lin­ear func­tion with the form i = v / R.

The poten­tial grav­i­ta­tion­al ener­gy of an object is a lin­ear func­tion of its height above ground.

There are sev­er­al phys­i­cal phe­nom­e­na that are char­ac­ter­ized by lin­ear behav­ior and that we might be inter­est­ed in implementing.

Conclusion

The lin­ear func­tion is one of the most basic func­tions but also one of the most useful.

The graph in the Carte­sian plane cor­re­sponds to a line in which we can iden­ti­fy a slope and an ordi­nate to the ori­gin, point in which the line cuts to the ver­ti­cal axis or abscissa.

We can use it to estab­lish lin­ear rela­tion­ships between dif­fer­ent para­me­ters of our game and rep­re­sent phys­i­cal phe­nom­e­na of lin­ear character.