Introduction
In previous entries we saw how to define matrices in programming and load data into them, in this article we will see how to multiply two matrices using two-dimensional arrays.
Initial data
We will start from two matrices “A” and “B” with preloaded data and we will analyze a method that will multiply two matrices that are sent as parameter and returns the result matrix.
In figure 1 we see the declaration of two 2×2 matrices and the loading of their data, then in lines 27 and 28 we make the calls to the method that is in charge of multiplying the matrices that are sent as parameters and returning the resulting matrix.

Algorithm for multiplying matrices in programming
The product of matrices is not commutative, so it matters the order in which the matrices are multiplied. Let’s consider that matrix A is on the left and multiply it by matrix B which is on the right.
The procedure to multiply two matrices consists of multiplying each element of the i-th row of the left matrix by each element of the j-th column of the right matrix and then adding these products, the result of that sum will be the ij-element of the resulting matrix. Therefore, in order to carry out the product of matrices, the condition that the number of columns of the left matrix equals to the number of rows of the right matrix must be fulfilled.
The result of the multiplication of matrices A and B will be another matrix that will have a number of rows equal to the number of rows in A and a number of columns equal to the number of columns in B.
Algorithm analysis
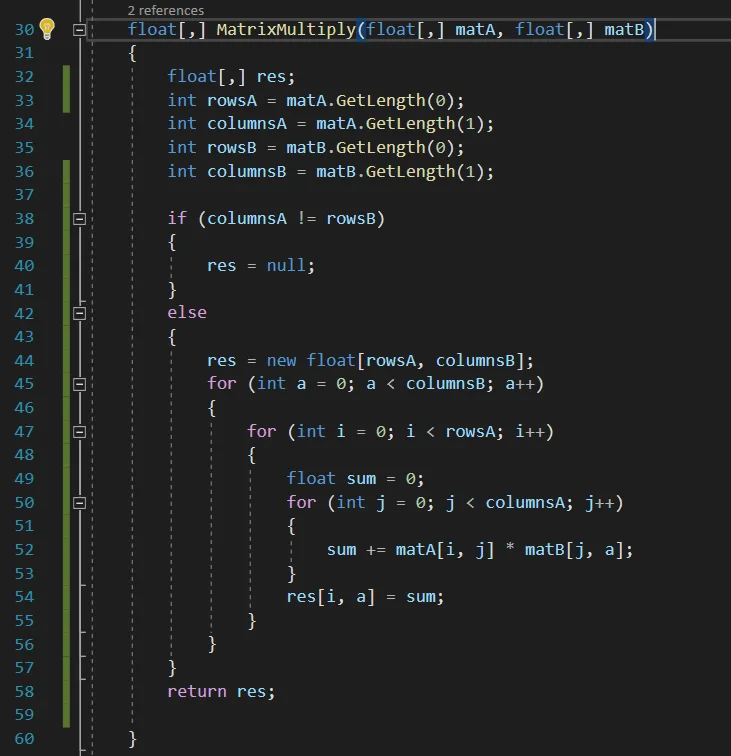
Figure 2 shows the implementation of an algorithm that multiplies two matrices that are sent as parameters. First the result matrix is declared and the sizes of both matrices are read, this is done in lines 32 to 36.
Then we check if it is possible to multiply both matrices, if it is not possible the result will be null, otherwise we proceed to solve the product of matrices.
The resulting matrix structure is created with the corresponding number of rows and columns (see the description of the procedure above). Then the three nested for loops shown in figure 2 are used to determine the value of each resulting element.