Introduction
In previous entries we saw how to define matrices in programming and load data into them, in this article we will see how to add and subtract two matrices using two-dimensional arrays.
To be able to add or subtract two matrices it is necessary that both have the same size, that is to say the same number of rows and the same number of columns, otherwise the operation cannot be solved. We will take this into account in our algorithm, at the time of performing the operation we will check that these conditions are met and if everything is correct the sum will be solved, otherwise the returned matrix will have a null value and this result can be used to make subsequent checks, for example if the resulting matrix is different from null we consider that the operation was successful.
Initial data
We will start from two matrices “A” and “B” with preloaded data and we will analyze a method that will perform the sum of two matrices that are sent as parameter and returns the result matrix.
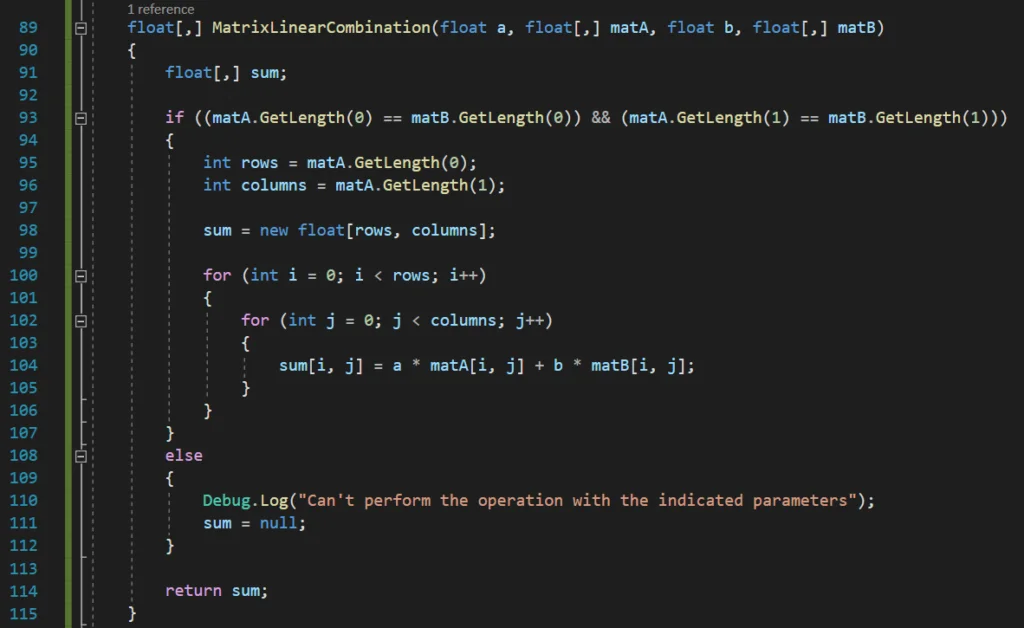
In figure 1 we see the declaration of two 2×2 matrices and the loading of their data, then in lines 28, 29 and 30 we make the calls to the methods that will be in charge of adding, subtracting or making a linear combination between the matrices that are sent as parameter, those methods will return the resulting matrix.
Algorithm to add two arrays in programming, C# language
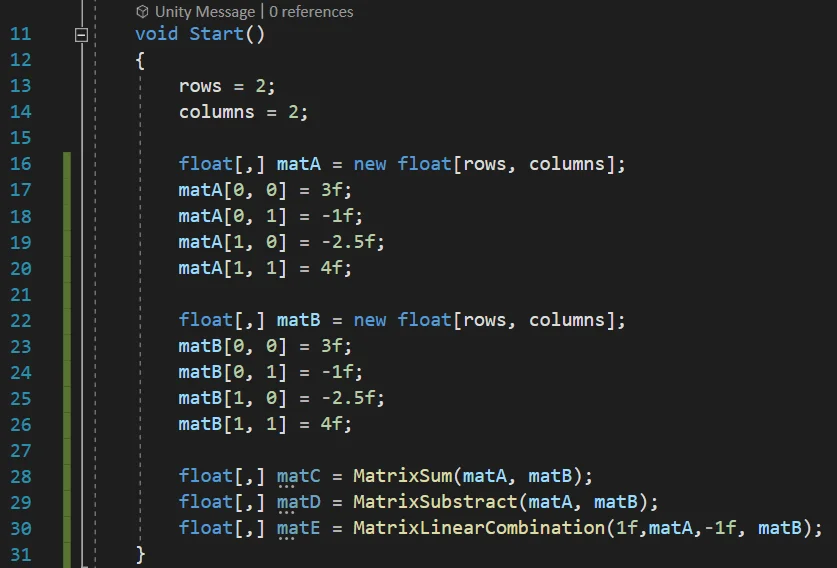
To make the sum of two matrices we must first make sure that both matrices have the same size, if this is correct we proceed to go through each element of the matrices and perform the sum element by element, assigning the result to a new matrix previously declared.
Analysis of the algorithm that performs the addition of two matrices
Between lines 30 and 56 we have defined a method that receives as parameters two two-dimensional arrays (“matA” and “matB”) and returns another two-dimensional array.
The result matrix is declared on line 32 and returned on line 55, at the end of the procedure.
Then in line 34 we have an IF statement to check if it is possible to solve the sum of the matrices, the condition is that the matrices match in number of rows and columns, if this is true we proceed to solve the sum, otherwise a message is printed on the console indicating that it is not possible to solve the operation and the result variable is assigned null (lines 51 and 52).
If the sum of matrices can be solved we will determine the number of rows and columns of the result matrix and we will create the data structure for that matrix, we do this in lines 36, 37 and 39 respectively.
The addition of the matrices is done element by element, therefore we will use two nested loops, the first one will go through each row and the inner loop will go through each column, so we will start with a row and go through each of the columns, at the end we will go to the next row. Inside the inner loop we simply solve the sum of the ij-elements of each matrix and assign it to the ij-element of the result matrix.
Algorithm to subtract two matrices in programming, C# language
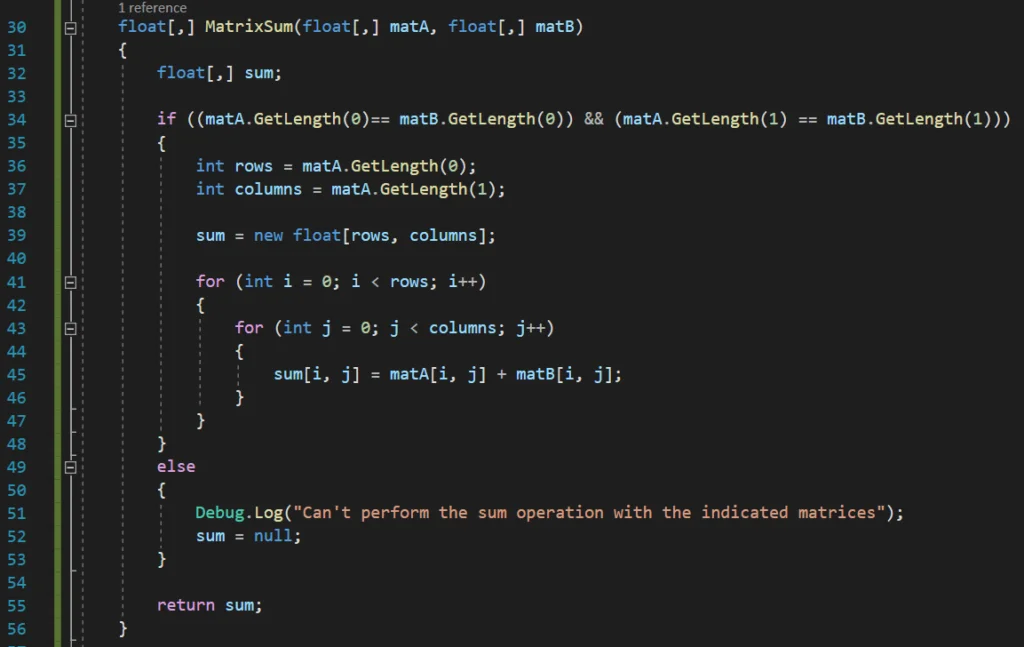
To subtract two matrices in programming, the algorithm is practically the same as the addition, only that when their elements are traversed, instead of adding them, they are subtracted, we can see an implementation of the algorithm in Figure 3.
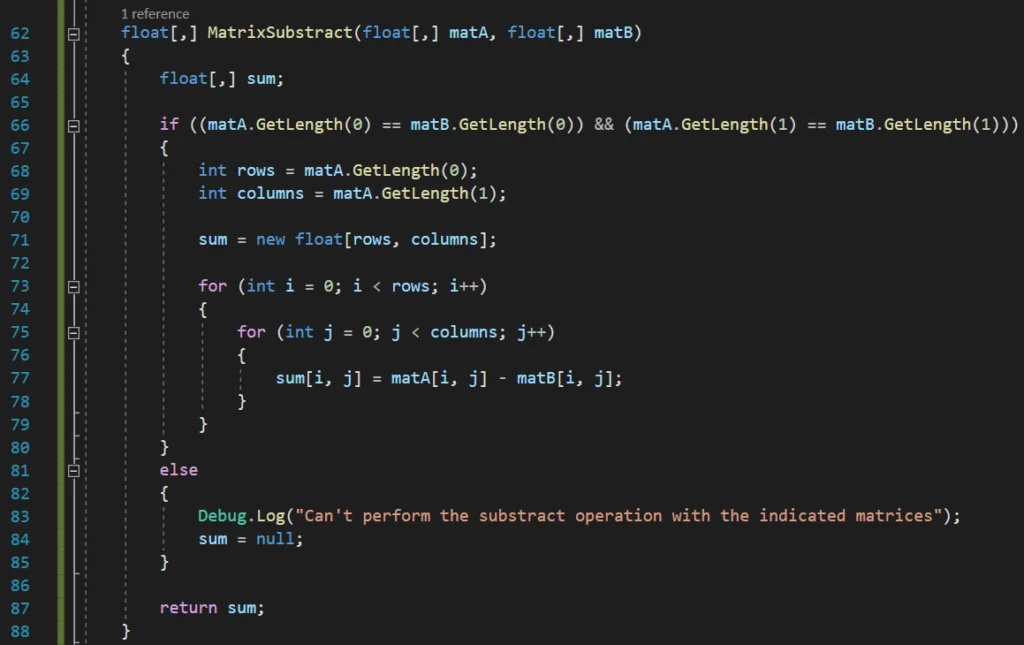
Algorithm to perform the linear combination of two matrices in programming, C# language.
Since the algorithms for adding and subtracting matrices are very similar, a function could be defined that performs a linear combination between the two matrices indicated together with their coefficients, i.e. it solves the operation:
MatrixC = a * MatrixA + b * MatrixB
In this way to perform the subtraction of matrix A minus matrix B we could call this function passing as parameter 1 for the coefficient that multiplies matrix A and -1 for the coefficient that multiplies matrix B, but we also have a function with higher capabilities. In Figure 4 we see the algorithm that solves the linear combination between both matrices.