CIRCUNFERENCIA - Cómo se define, ecuación y gráfica

Introducción

En este artículo vamos a estudiar la circunferencia como figura geométrica, cuáles son sus características y su ecuación matemática. Además vamos a ver cómo calcular su perímetro y área.

Definición de una circunferencia

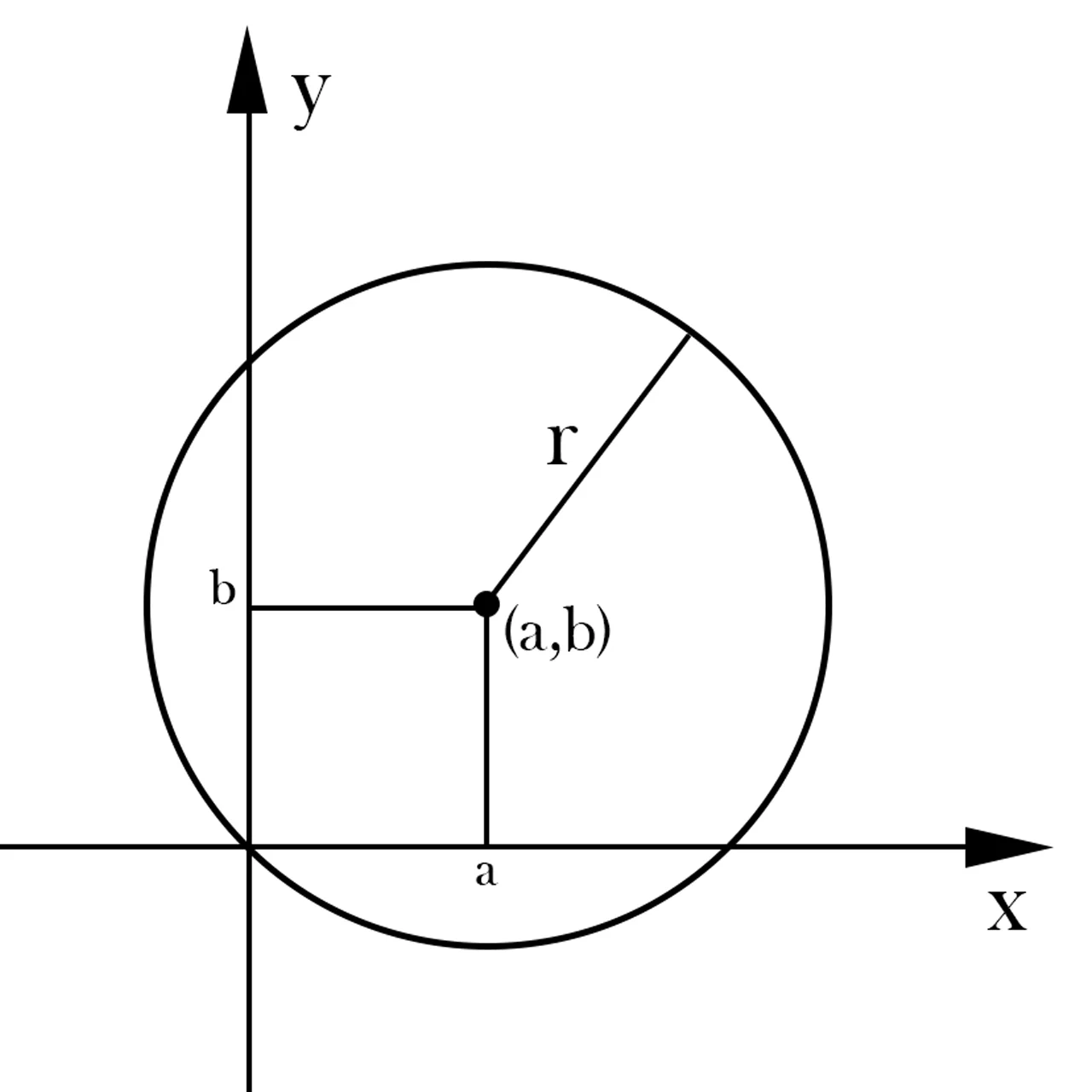
Una circunferencia es una figura geométrica en la cual todos sus puntos se encuentran a la misma distancia de un determinado punto llamado centro, dicha distancia se conoce como radio de la circunferencia. En la figura 1 vemos el gráfico de una circunferencia genérica cuyo centro se encuentra en el punto (a,b) y tiene un radio r.

grafico de una circunferencia generica de radio r y centro en el punto a,b. figura geometrica cuyos puntos equidistan de un punto llamado centro una distancia llamada radio — Fig. 1: Gráfico de una circunferencia de radio R centrada en (a,b).

Ecuación de una Circunferencia

Conociendo la expresión matemática de una circunferencia podremos dibujarla en el plano cartesiano y posteriormente utilizarla en nuestros proyectos de programación y desarrollo de videojuegos.

Coordenadas cartesianas

La expresión que define una circunferencia en coordenadas cartesianas es la siguiente:

(1) $\begin{equation*} ( x - a )^2+( y - b )^2=R^2\end{equation*}$

Donde R es el radio de la circunferencia y su centro se sitúa en el punto (a,b) del plano cartesiano.

En este caso para dibujar la circunferencia debemos conocer el rango de valores de las variables X e Y. Por ejemplo consideremos el círculo unidad centrado en (0,0):

(2) $\begin{equation*} x^2+y^2=1\end{equation*}$

Si dibujamos un círculo de radio 1 con centro en (0,0) podemos ver que tanto los valores de X como de Y van a estar en el intervalo [-1,1]. Al elegir un valor de ese intervalo y asignarlo a una de las variables podremos despejar la ecuación y obtener el valor de la otra variable.

Coordenadas paramétricas

También puede ser útil la expresión de una circunferencia en el sistema de coordenadas paramétricas ya que al estar definido con funciones periódicas, el rango de variación del parámetro es infinito. La expresión de un círculo está dada por el siguiente sistema de ecuaciones.

x=a+r.cos(t)

y=b+r.sin(t)

(3) $\begin{equation*} t \in [0,2π ] \end{equation*}$

Haciendo variar el parámetro t entre 0 y 2π obtenemos todos los puntos de la circunferencia.

Como mencionamos antes el parámetro t puede tomar valores de menos infinito a más infinito y siempre va a devolver algún punto de la circunferencia, debido a que los senos y cosenos son funciones periódicas.

Circunferencia y funciones matemáticas

Hay que tener en cuenta que no existe una función matemática que defina el círculo ya que por su definición, una función es una expresión en la que se cumple que, para cada valor de la variable independiente, existe un único valor para la variable dependiente. Por lo tanto la circunferencia no es una función matemática.

En otras palabras, para que un gráfico pueda corresponder a una función matemática debemos poder trazar una línea vertical en cualquier parte del gráfico y ésta línea debería corta a la función en un único punto. Esto no ocurre en el círculo, ya que si tomamos por ejemplo un círculo de radio R centrado en el origen (0,0), la recta coincidente con el eje Y corta al círculo en dos puntos.

Algo que sí sería válido es descomponer el gráfico de la circunferencia en dos partes, un semicírculo superior y uno inferior y encontrar las expresiones matemáticas cuyos gráficos se corresponden con esos semi círculos. Esto lo que podemos hacer despejando la variable y en la ecuación 1 de mas arriba.

(4) $\begin{equation*} |(y - b)|= \sqrt{ R^2 - (x-a)^2 }\end{equation*}$

El valor absoluto surge porque tomamos la raíz cuadrada de una expresión que está elevada al cuadrado, esto da lugar a dos valores posibles para esa expresión, uno positivo y otro negativo, que son los que definen el semi círculo inferior y superior de la circunferencia.

Semicírculo superior

La expresión de la función que representa el semi círculo superior de una circunferencia genérica es:

(5) $\begin{equation*} y = \sqrt{ R^2 - (x-a)^2 } + b\end{equation*}$

Semicírculo inferior

La expresión de la función que representa el semi círculo inferior de una circunferencia genérica es:

(6) $\begin{equation*} y = - \sqrt{ R^2 - (x-a)^2 } + b\end{equation*}$

Perímetro de una circunferencia

El perímetro de un círculo es la longitud de su frontera, imaginemos que hacemos una marca en un punto del círculo, colocamos ese punto en el 0 de una recta y lo hacemos girar hacia adelante, el punto donde la marca vuelve a tocar la recta es el valor del perímetro de la circunferencia. Matemáticamente se puede calcular como:

(7) $\begin{equation*} per = 2 . \pi . r\end{equation*}$

PI tiene un valor aproximado de 3.1415 y «r» es el radio de la circunferencia.

Área de una circunferencia

El área de un círculo es el resultado de la multiplicación del número π por el radio de la circunferencia al cuadrado. Matemáticamente:

(8) $\begin{equation*} área = \pi . r^2\end{equation*}$

Aplicaciones de la circunferencia en programación

VÍDEO: Determinar puntos cercanos a otro punto

Debido a que la circunferencia es el conjunto de puntos que se encuentran a una cierta distancia llamada «radio» a un punto llamado «centro», si nos paramos en el centro de la circunferencia y analizamos la distancia de un punto cualquiera al centro de la circunferencia podemos saber si el punto está fuera, sobre o dentro de la circunferencia.

Es como si el radio de la circunferencia definiera una frontera, todos los objetos que estén a una distancia menor al radio de circunferencia se encontrarán en el interior de la misma, si el punto está a una distancia mayor al radio sabemos que está fuera de la circunferencia y si la distancia es igual al radio el punto está sobre la circunferencia.

En el vídeo que se encuentra a continuación utilizo la ecuación paramétrica de la circunferencia para dibujar un círculo alrededor de un objeto, en los primeros minutos del vídeo se puede ver el código para determinar el i-ésimo punto de un círculo de radio «distance» y «circleSubdivisions» subdivisiones, esta es la instrucción:

Vector3 circlePoint = new Vector3(distanceMathf.Cos(2Mathf.PIi/circleSubdivisions)+ targetObject.position.x, 0f, distanceMathf.Sin(2 * Mathf.PI * i / circleSubdivisions) + targetObject.position.z);

SUSCRÍBETE AL CANAL