Introduction

In this arti­cle we are going to study the geo­met­ric fig­ure cir­cle, its char­ac­ter­is­tics and math­e­mat­i­cal equation.

Definition of a circle

A cir­cle is a geo­met­ric fig­ure in which all its points are at the same dis­tance from a giv­en point called the cen­ter, this dis­tance is known as the radius of the circle.

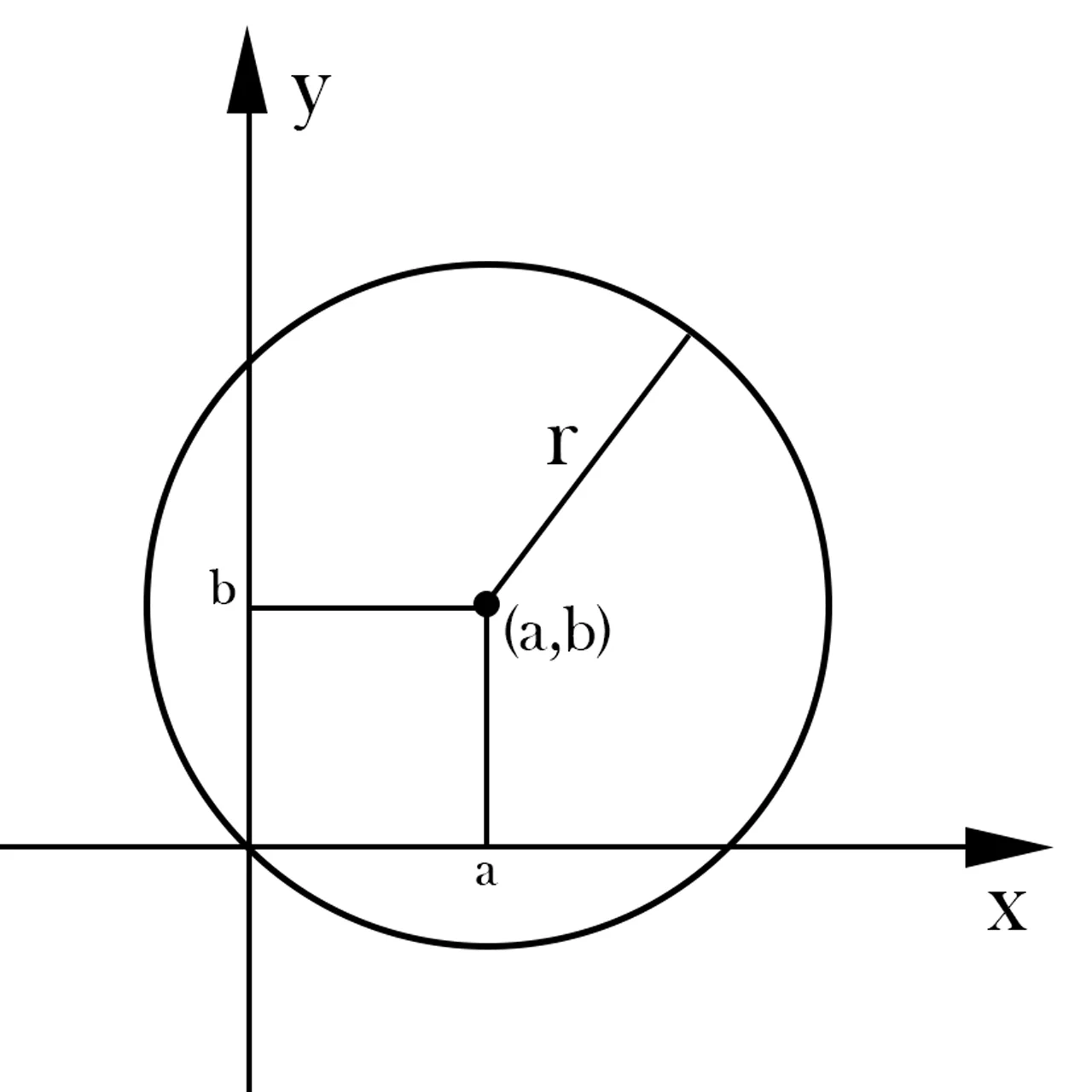
Equation of a Circle

Know­ing the math­e­mat­i­cal expres­sion of a cir­cum­fer­ence we will be able to draw it in the Carte­sian plane and lat­er use it in our projects of pro­gram­ming and devel­op­ment of videogames.

Cartesian coordinates

The expres­sion that defines a cir­cle in Carte­sian coor­di­nates is the following:

(1)  

Where R is the radius of the cir­cum­fer­ence and its cen­ter is locat­ed at point (a,b) of the Carte­sian plane.

In this case to draw the cir­cle we must know the range of val­ues of the vari­ables X and Y. For exam­ple, let's con­sid­er the cir­cle unit cen­tered in (0,0):

(2)  

If we draw a cir­cle of radius 1 with cen­ter in (0,0) we can see that both the val­ues of X and Y will be in the inter­val [-1,1]. By choos­ing a val­ue from that inter­val and assign­ing it to one of the vari­ables we will be able to clear the equa­tion and obtain the val­ue of the oth­er variable.

Parametric coordinates

The expres­sion of a cir­cum­fer­ence in the para­met­ric coor­di­nate sys­tem may also be use­ful, since the range of vari­a­tion of the para­me­ter is infi­nite since it is defined with peri­od­ic func­tions. The expres­sion of a cir­cle is giv­en by the fol­low­ing sys­tem of equations.

By vary­ing the t para­me­ter between 0 and 2π we obtain all the points of the circumference. 

As we men­tioned before the para­me­ter t can take val­ues from less infi­nite to more infi­nite and will always return some point of the cir­cum­fer­ence, because the sinus­es and cosines are peri­od­ic functions.

Circle and mathematical functions

It must be borne in mind that there is no math­e­mat­i­cal func­tion that defines the cir­cle since, by def­i­n­i­tion, a func­tion is an expres­sion in which it is ful­filled that, for each val­ue of the inde­pen­dent vari­able, there is only one val­ue for the depen­dent variable. 

In oth­ers for it to be a func­tion we must be able to draw a ver­ti­cal line any­where on the graph and this should cut the func­tion into a sin­gle point. This does not hap­pen in the cir­cle, since if we take for exam­ple the line coin­ci­dent with the Y axis, we see that it cuts the cir­cle unit cen­tered in (0,0) in two points.

What we can do is clear the vari­able and in equa­tion 1.

(4)  

The absolute val­ue aris­es when tak­ing the square root of an expres­sion that is ele­vat­ed to the square, this gives rise to two pos­si­ble val­ues for that expres­sion, one pos­i­tive and the oth­er neg­a­tive, that define the low­er and upper cap of the circumference.

Semicircle — Concave from below

The expres­sion of the func­tion that rep­re­sents the top semi­cir­cle of a gener­ic cir­cle is:

(5)  

Semicircle — Concave from above

The expres­sion of the func­tion that rep­re­sents the bot­tom semi­cir­cle of a gener­ic cir­cle is: 

(6)  

Perimeter of a circle

The perime­ter of a cir­cle is the length of its bound­ary, let's imag­ine that we make a mark in a point of the cir­cle, we place that point in the 0 of a line and we make it turn for­ward, the point where the mark touch­es the line again is the val­ue of the perime­ter of the cir­cum­fer­ence. Math­e­mat­i­cal­ly it can be cal­cu­lat­ed as:

(7)  

Pi has an approx­i­mate val­ue of 3.1415 and r is the radius of the circumference.

Area of a circle

The area of a cir­cle is the result of mul­ti­ply­ing the num­ber Pi by the radius of the cir­cle squared. Mathematically:

(8)