{ PLANO CARTESIANO } - Sistema de Coordenadas. Aplicación en Unity

Introducción

El sistema de coordenadas cartesianas recibe su nombre en honor al filósofo y matemático René Descartes, considerado el creador de la geometría analítica. Este sistema nos permite representar puntos tanto en el plano como en el espacio.

¿Qué es un plano cartesiano?

El plano cartesiano está definido por dos rectas perpendiculares entre sí, una horizontal y otra vertical, estas rectas se conocen como ejes cartesianos. Utilizando estos ejes podemos identificar cualquier punto del plano con un único par ordenado de números.

El eje horizontal se lo conoce como eje de ABSCISAS y normalmente es conocido como eje x (aunque podría usarse cualquier letra). El eje vertical es conocido como eje de ORDENADAS y normalmente es el eje y.

El punto donde se cortan los ejes de abscisas y ordenadas se conoce como ORIGEN de coordenadas o simplemente origen y es el punto (0,0) en el plano y (0,0,0) en el espacio.

En la siguiente figura se muestra un plano cartesiano con el punto (2,1) graficado.

representacion en plano cartesiano con el punto 2 1 representado — *Fig. 1: Plano cartesiano xy con el punto (2,1) representado.*

Cuadrantes del plano cartesiano

Los cuadrantes son regiones características del plano definidas por los cambios de signos en los ejes coordenados. Son cuatro cuadrantes, el primero es la región superior derecha y se enumeran en sentido antihorario.

Como se observa en la figura 2, los cuadrantes están definidos en las siguientes regiones.

Primer cuadrante: { x > 0 , y > 0 }

Segundo cuadrante: { x < 0 , y > 0 }

Tercer cuadrante: { x < 0 , y < 0 }

Cuarto cuadrante: { x > 0 , y < 0 }

Representar funciones en el plano cartesiano

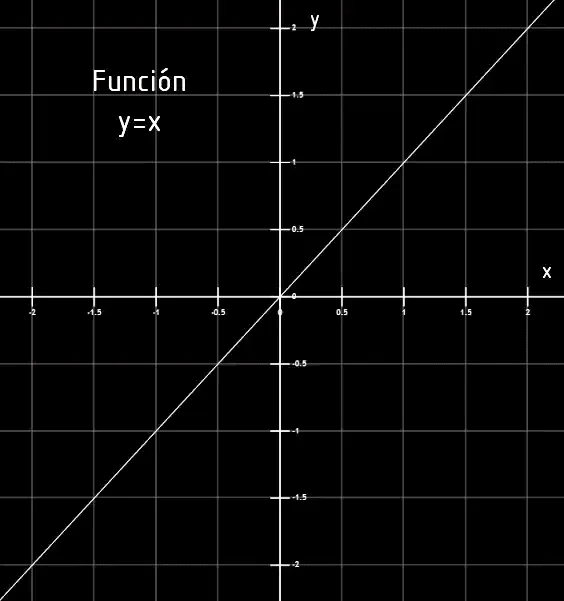
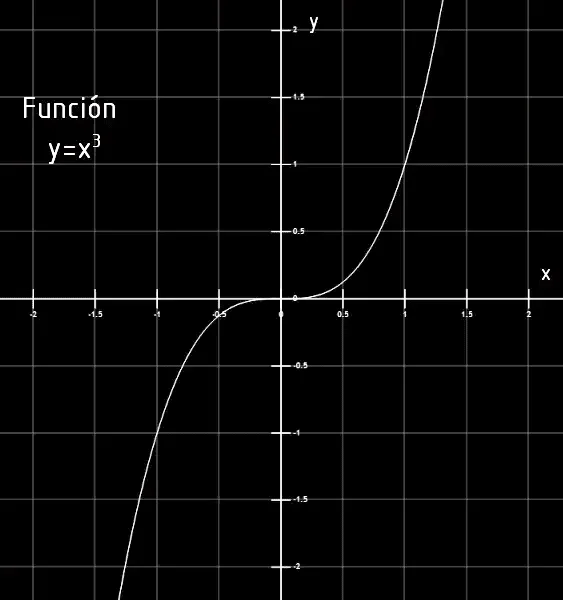
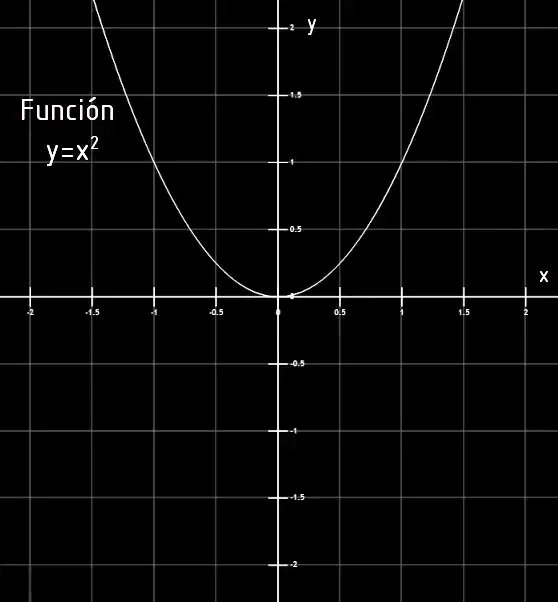
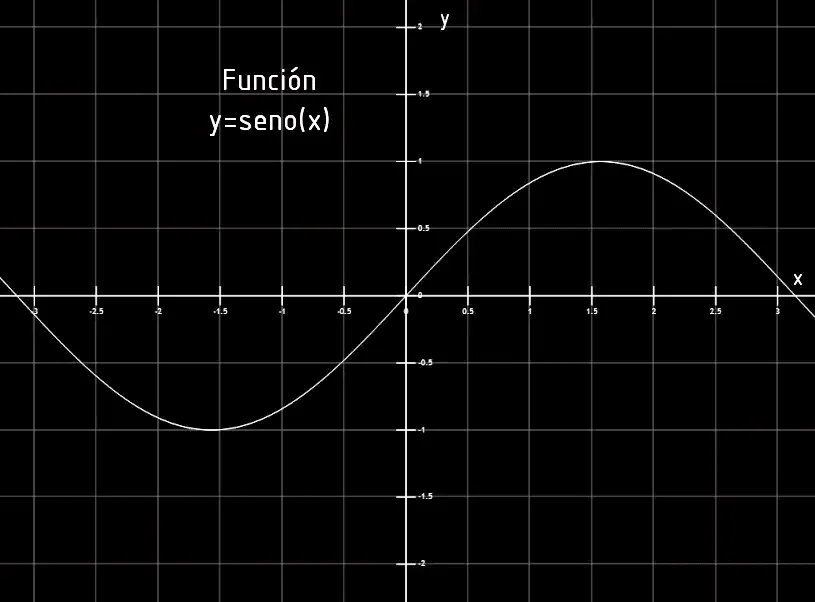
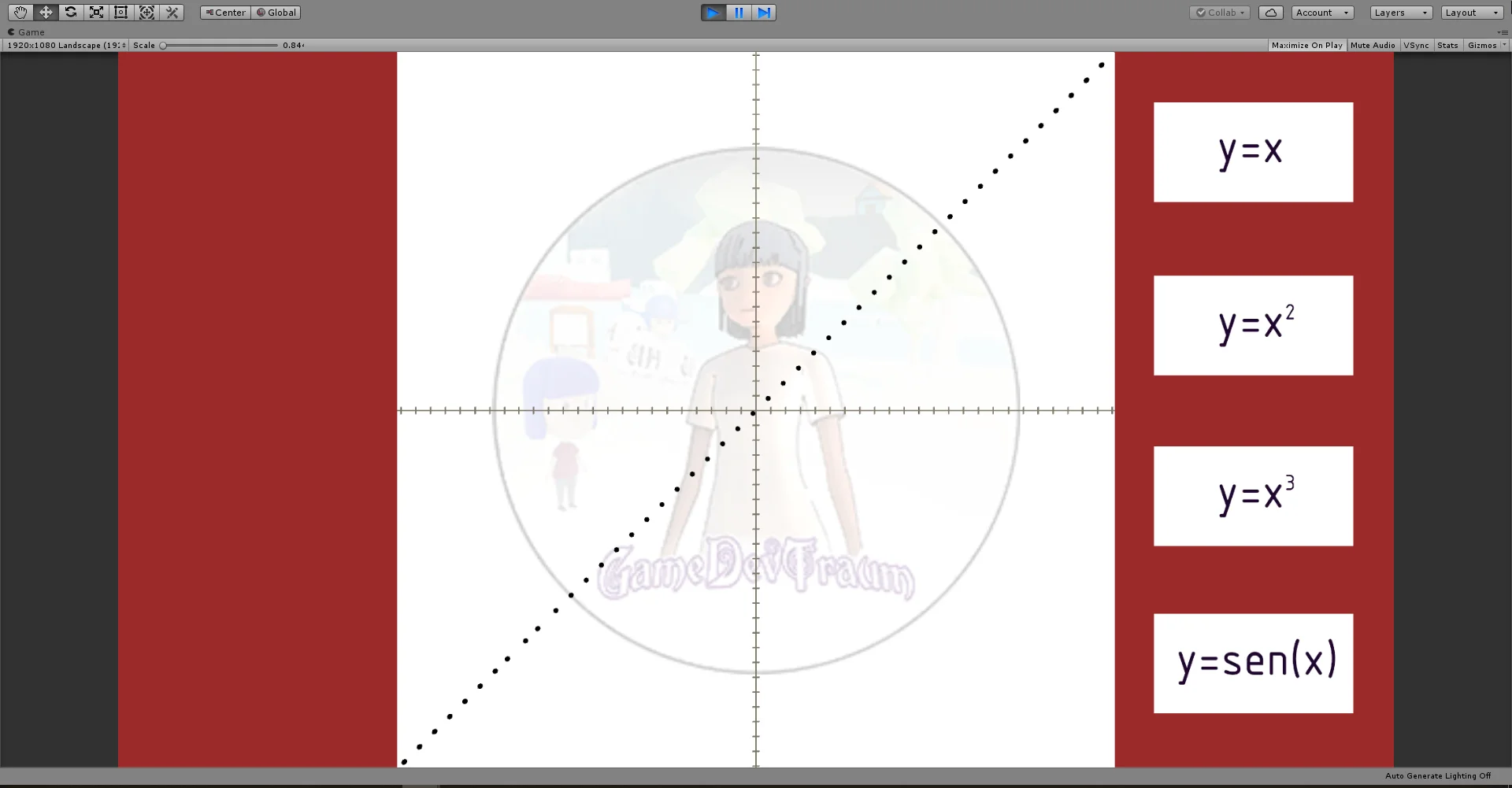
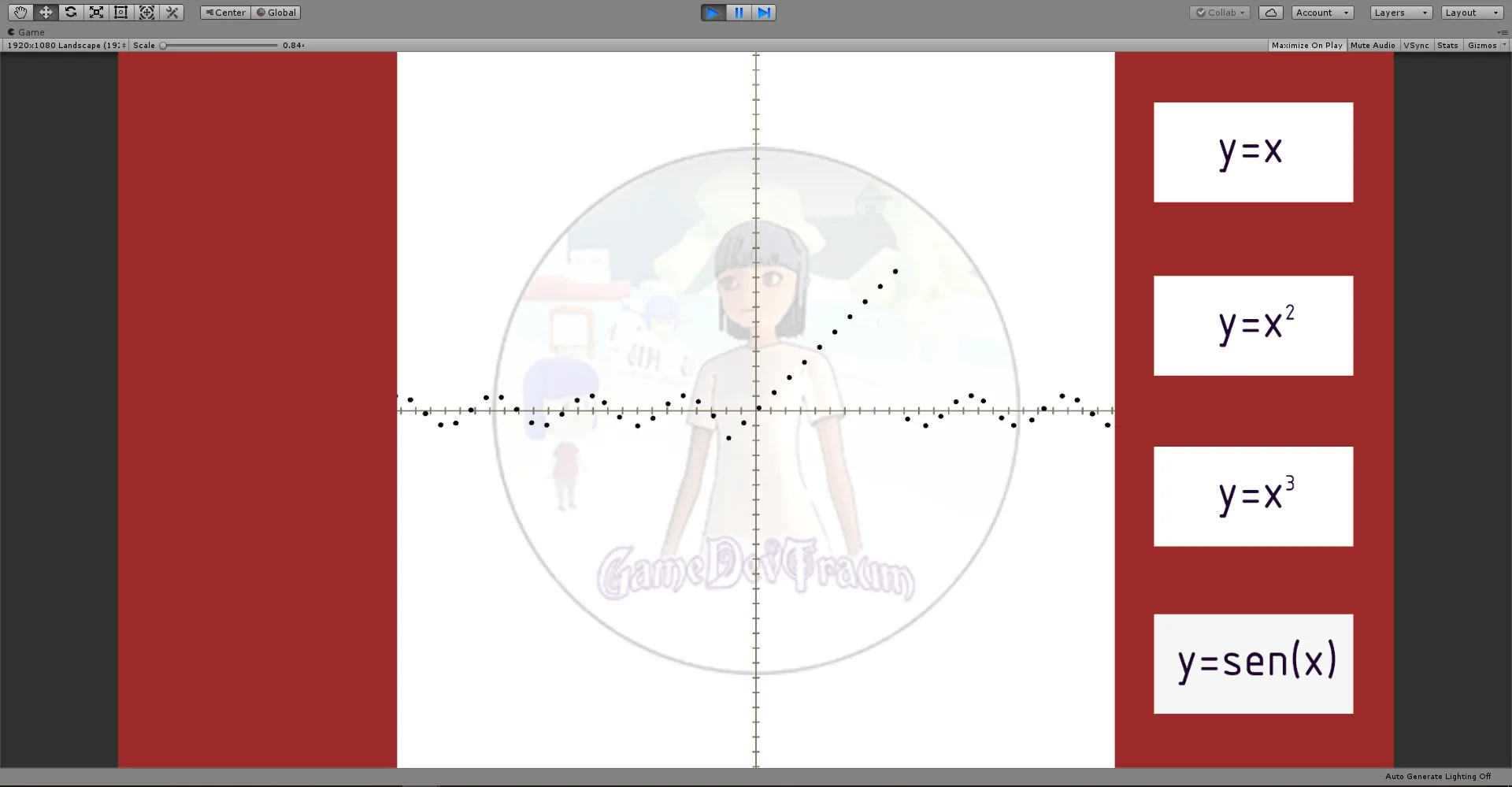
El plano cartesiano además nos sirve para representar funciones, es decir reglas que asignan cada punto del eje x a un punto del eje y. En las figuras 3 a 6 se muestran algunos ejemplos de gráficos de funciones en el plano cartesiano.

grafico de una funcion lineal en el plano cartesiano. — *Fig. 3: Gráfico de una función lineal.*

grafico de una funcion cubica en el plano cartesiano. — *Fig. 5: Gráfico de una función cúbica.*

grafico de una funcion cuadratica o parabola en el plano cartesiano. — *Fig. 4: Gráfico de una función cuadrática o parábola.*

grafico de una funcion seno de x en el plano cartesiano. — *Fig. 6: Gráfico de una función seno de x.*

Sistema cartesiano en Unity

Las coordenadas cartesianas se utilizan en varios lugares en Unity, por ejemplo para definir la posición de un GameObject en el plano o el espacio. Pero para el propósito quise hacer un graficador de funciones simple utilizando esferas que se mueven en el eje x y su posición en el eje y se calcula utilizando la expresión de la función.

Los botones nos permiten cambiar la expresión de la función

escena en unity en la que se observa esferas formando una funcion lineal — *Fig. 7: Las esferas se mueven de acuerdo a una función lineal.*

escena en unity en la que se observa esferas formando una funcion cuadratica — *Fig. 9: Las esferas se mueven de acuerdo a una función cuadrática.*

escena en unity en la que se observa esferas formando una funcion senoidal — *Fig. 8: Las esferas se mueven de acuerdo a una función senoidal.*

escena en unity en la que se observa esferas formando una funcion senoidal en un tramo y lineal en otro — *Fig. 10: Las esferas se mueven de acuerdo a una función senoidal en un tramo y lineal en otro.*

Conclusión

Las coordenadas rectangulares se utilizan con frecuencia en Unity.

Comprender cómo se utiliza el plano cartesiano para representar puntos y funciones en el plano, junto con conocimientos de geometría analíticas nos puede ayudar a crear nueva e interesantes soluciones.