Introducción
Un vector es una herramienta matemática que nos permite representar magnitudes en las que no sólo importa la intensidad (o módulo), sino también la dirección y el sentido en la que están aplicadas. Los vectores son muy útiles en el desarrollo de juegos, ya que nos permiten definir direcciones para el movimiento, hacer trazado de rayos, entre otras aplicaciones.
El ejemplo más simple y quizás más cotidiano que se me ocurre es el de una fuerza. Las fuerzas son magnitudes vectoriales, no sólo importa la intensidad de la fuerza que se aplica, sino también la dirección y el sentido.
Si por ejemplo cambiamos el sentido de la fuerza que le aplicamos a un objeto, el objeto se moverá en la dirección contraria o disminuirá su velocidad.
Otros ejemplos de magnitudes vectoriales pueden ser el torque, el momento angular, la velocidad. En electricidad y magenitsmo tenemos el campo eléctrico en un punto, el vector de Poynting.
Vectores en el plano y en el espacio
Por cuestiones prácticas vamos a ver el caso de vectores en el plano y en el espacio, es decir vectores de dos y tres componentes respectivamente.
Matemáticamente
Usualmente un vector se identifica usando una letra con una flecha en la parte superior.
Hay distintos tipos de notaciones, una de ellas es escribir las componentes del vector entre paréntesis y separadas con coma. En el plano usamos dos componentes y en el espacio tres.
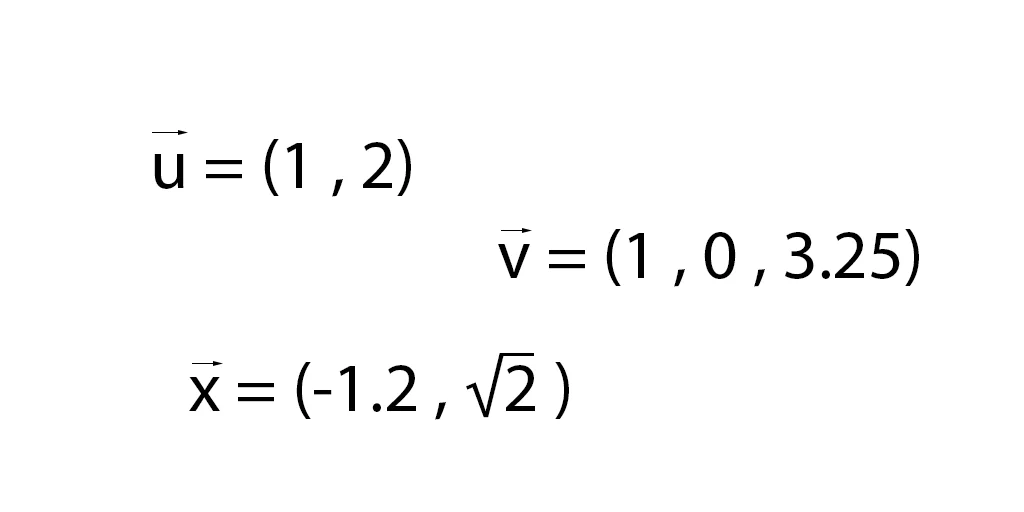
Representación gráfica de vectores
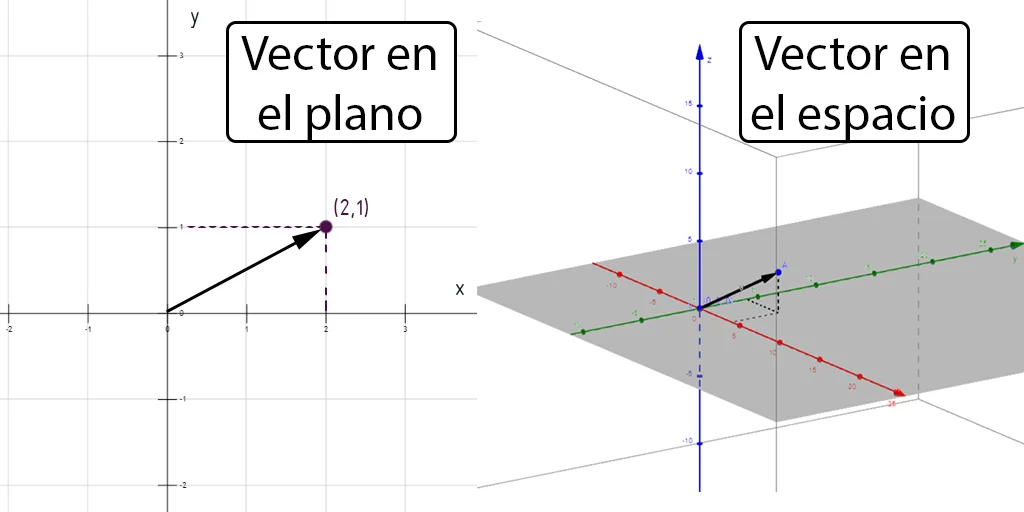
El valor del vector representa el punto final de una flecha que parte desde el origen de coordenadas (es decir (0,0) en el plano y (0,0,0) en el espacio), hasta la coordenada que indica el vector. Como se ilustra en la figura 2.
Hace un tiempo escribí un artículo sobre sistema cartesiano, puedes leerlo haciendo clic aquí.
Características de un vector
Componentes de un vector
Las componentes son los valores reales para cada eje del sistema de coordenadas.
En el plano un vector tiene dos componentes, generalmente x e y, en el espacio necesitamos tres componentes, en general se llaman x, y y z.
Módulo o Norma de un vector
El módulo o norma de un vector nos habla del tamaño del vector, la magnitud o intensidad que tiene, en otras palabras es cuánto mide el vector desde el origen hasta el punto final.
Para calcular el módulo se utiliza el teorema de Pitagoras sobre los triángulos rectángulos que forma el vector con los ejes coordenados. Esto suena algo complicado pero las fórmulas son simples, en la figura 3 vemos el cálculo de la norma de un vector en el plano y en el espacio. Fórmula con ejemplos.
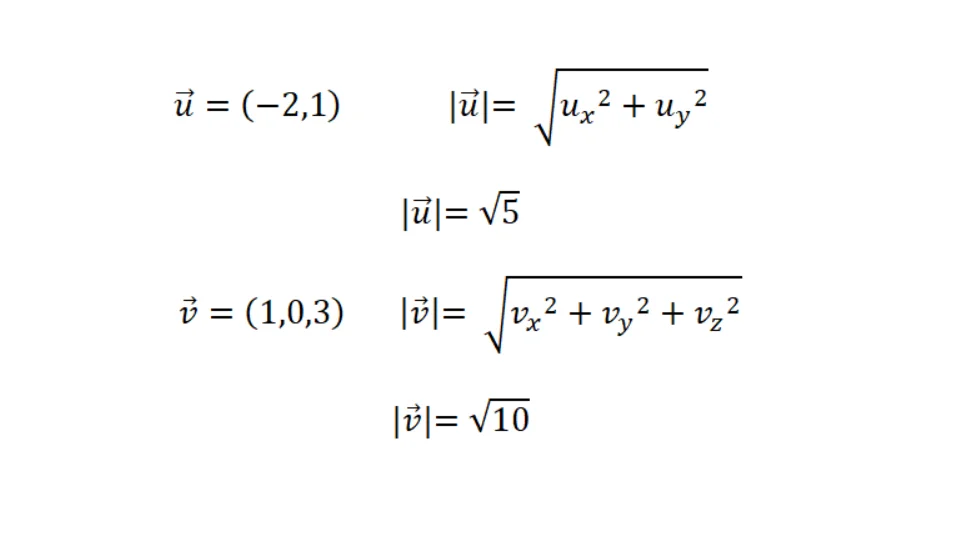
Dirección de un vector
Esto habla de la orientación del vector en el plano o en el espacio. Esto nos permite calcular ángulos respecto a los ejes coordenados utilizando triángulos rectángulos y senos y cosenos.
Dado un vector podemos encontrar una única recta que lo contiene.
Acá empezamos a ver la utilidad de saber sobre vectores para programar videojuegos, con los vectores podemos representar movimientos en una determina dirección o calcular la trayectoria de un proyectil por ejemplo.
Sentido de un vector
Dada una dirección para el vector, dijimos que existe una única recta que lo contiene, sin embargo el vector podría estar apuntando hacia un lado o hacia el otro de la recta. Con el sentido solucionamos esta ambigüedad.
Para cambiar el sentido de un vector basta con multiplicar por -1 todas sus componentes.
Vector en matemática vs Vector en programación
En programación también existe un tipo de datos que se conoce como vectores, arreglos o arrays. Sin embargo esto hace referencia a una estructura de programación en la que podemos ordenar datos del mismo tipo y utilizarlos para resolver algoritmos.
Podemos modelar vectores matemáticos utilizando arrays, sin embargo los arrays pueden contener cadenas de texto por ejemplo.
Vectores matemáticos en Unity
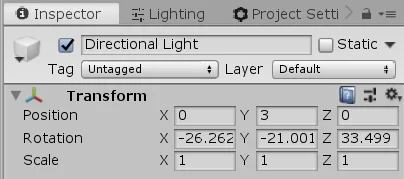
En Unity hay varios componentes que utilizan vectores, el más simple de todos es el componente Transform que determina la posición, rotación y escala de un GameObject en Unity.
Para esto utiliza tres vectores de tres dimensiones. En la figura 4 podemos visualizar estos vectores en el inspector. Unity le da a las componentes del vector el nombre x, y y z.
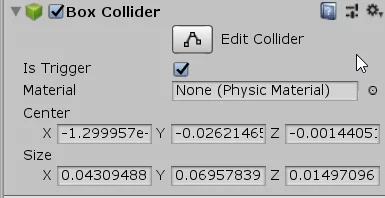
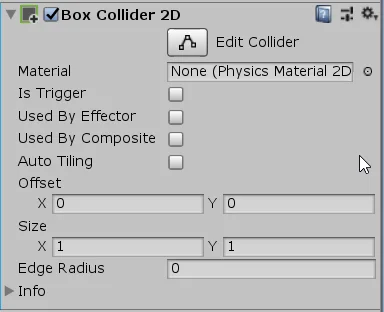
Otros componentes como los Colliders utilizan vectores para el dibujado del Collider, definir su posición y su tamaño. En la figura 5 vemos un ejemplo de Collider en tres dimensiones en los que se usan vectores de tres componentes y en la figura 6 un ejemplo de Collider 2D en el que se utilizan vectores de dos componentes.
Además de las componentes con las que cuenta Unity, en nuestros Script podemos crear vectores para utilizar en nuestros algoritmos.
El nombre del objeto con el que nos referimos a estos vectores en un Script C# para Unity es Vector2 y Vector3. Podemos observar algunos ejemplos en la figura 7.
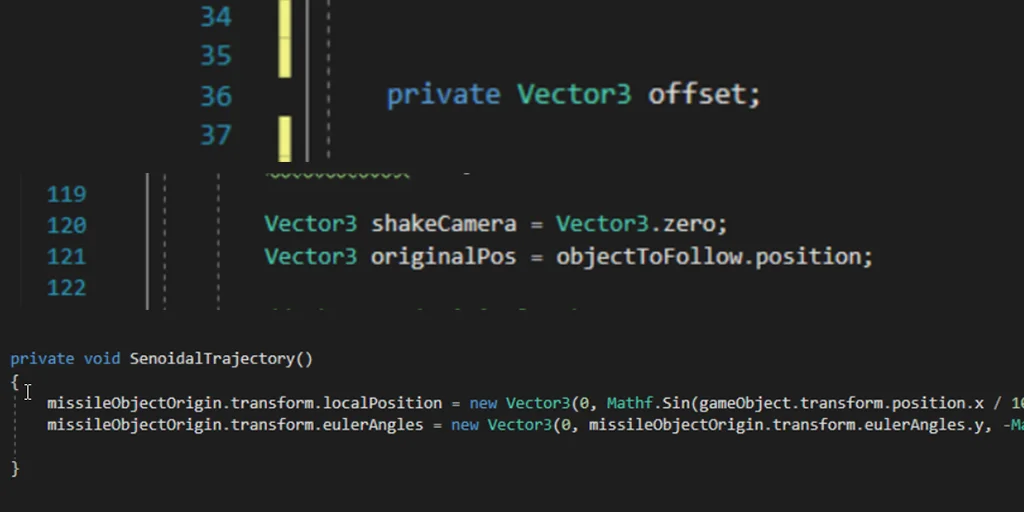
Un vídeo sobre introducción a los VECTORES en lenguaje C#
Conclusión
Los vectores en matemática son una herramienta útil para representar trayectorias, fuerzas
Un vector tiene un módulo que determina su tamaño, una dirección que determina su orientación en el espacio y un sentido dentro de esa dirección.
Dado un vector podemos encontrar una única recta que lo contiene.
