Introduction

A vec­tor is a math­e­mat­i­cal tool that allows us to rep­re­sent mag­ni­tudes in which not only the inten­si­ty (or mod­u­lus), but also the direc­tion and direc­tion in which they are applied are important. 

The vec­tors are very use­ful in the devel­op­ment of games, they allow us to define direc­tions for move­ment, do ray trac­ing, among oth­er applications.

The sim­plest and per­haps the most every­day exam­ple I can think of is that of a force. Forces are vec­tor mag­ni­tudes, not only does the amount of force applied mat­ter, but also direc­tion and meaning. 

If, for exam­ple, we change the direc­tion of the force we apply to an object, the object will prob­a­bly move in the oppo­site direction.

Oth­er exam­ples of vec­tor mag­ni­tudes can be torque, angu­lar momen­tum, veloc­i­ty. In elec­tric­i­ty and magenithm we have the elec­tric field at one point, the Poynt­ing Vec­tor.

Vectors in the plane and in space

For prac­ti­cal rea­sons we are going to look at the case of vec­tors in the plane and in space, i.e. vec­tors of two and three com­po­nents respectively.

Mathematically

Usu­al­ly a vec­tor is iden­ti­fied by a let­ter with an arrow at the top. 

There are dif­fer­ent types of nota­tions, one of them is to write the com­po­nents of the vec­tor in paren­the­ses and sep­a­rat­ed with com­ma. In the plane we use two com­po­nents and in the space three.

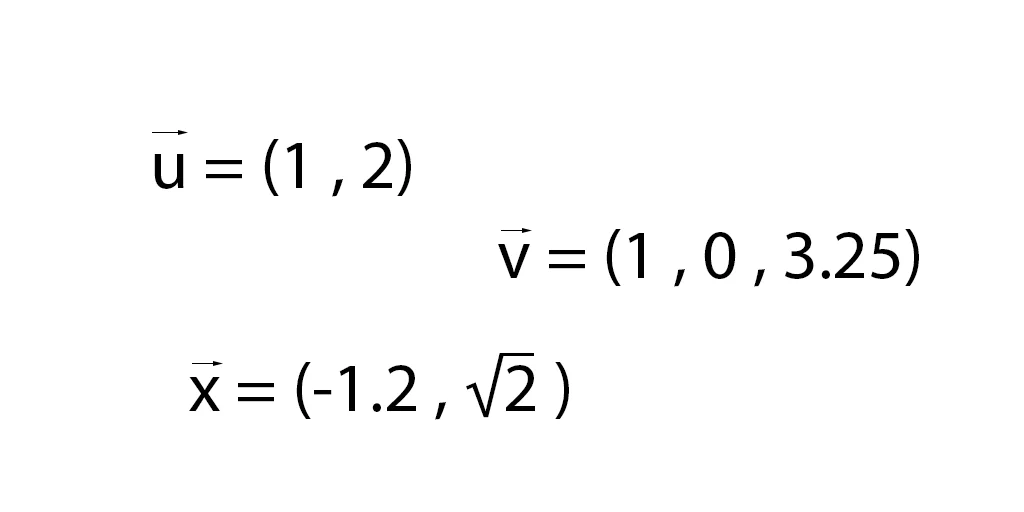
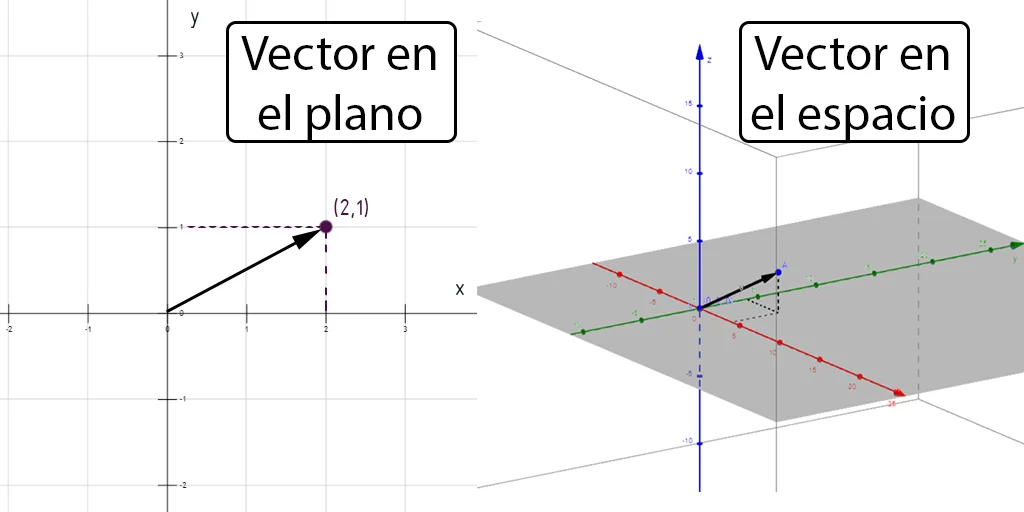
Graphic Representation

The val­ue of the vec­tor rep­re­sents the final point of an arrow start­ing from the ori­gin of coor­di­nates (i.e. (0.0) in the plane and (0.0.0) in space), to the coor­di­nate indi­cat­ed by the vec­tor. As illus­trat­ed in fig­ure 2.

Characteristics of a vector

Components

The com­po­nents are the actu­al val­ues for each axis of the coor­di­nate system. 

In the plane a vec­tor has two com­po­nents, gen­er­al­ly x and y, in space we need three com­po­nents, in gen­er­al they are called x, y and z. 

Magnitude

The mod­ule, norm or mag­ni­tude of a vec­tor tells us about the size of the vec­tor, the mag­ni­tude or inten­si­ty it has, in oth­er words is how much the vec­tor mea­sures from the ori­gin to the final point.

To cal­cu­late the mod­ule, Pitago­ras' the­o­rem is used on the right tri­an­gles formed by the vec­tor with the coor­di­nate axes. This sounds some­what com­pli­cat­ed but the for­mu­las are sim­ple, in fig­ure 3 we see the cal­cu­la­tion of the norm of a vec­tor in the plane and in space. For­mu­la with examples.

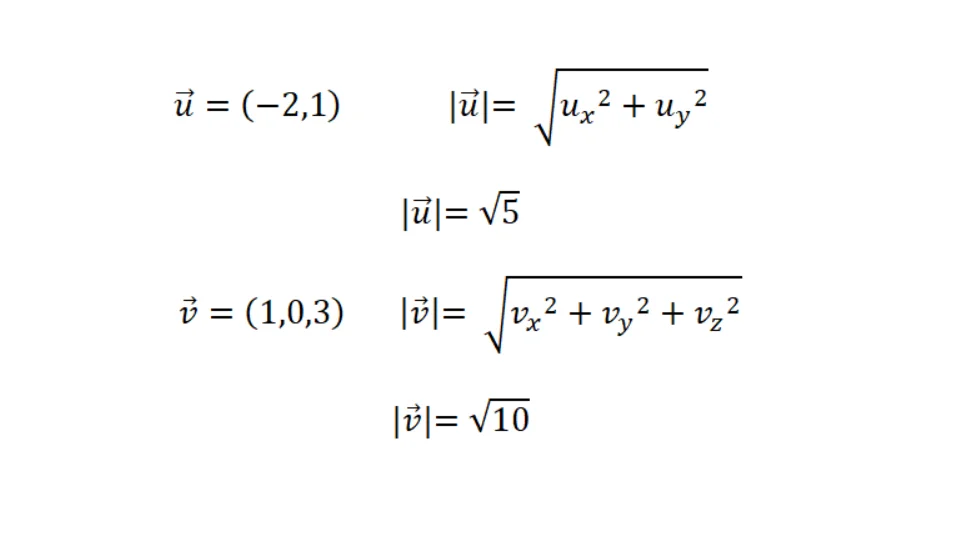
Orientation

The ori­en­ta­tion of the vec­tor in the plane or in space. This allows us to cal­cu­late angles with respect to coor­di­nate axes using right tri­an­gles, sinus­es and cosines.

Giv­en a vec­tor we can find a sin­gle line that con­tains it.

Here we begin to see the use­ful­ness of know­ing about vec­tors to pro­gram video games, with the vec­tors we can rep­re­sent move­ments in a deter­mined direc­tion or cal­cu­late the tra­jec­to­ry of a pro­jec­tile for example.

Sense

Giv­en a direc­tion for the vec­tor, we said that there is only one line that con­tains it, how­ev­er the vec­tor could be point­ing to one side or the oth­er of the line. With mean­ing we solve this ambiguity.

To change the direc­tion of a vec­tor it is enough to mul­ti­ply by ‑1 all its components.

Vector in mathematics vs Vector in programming

In pro­gram­ming there is also a type of data known as vec­tors, arrays or arrays. How­ev­er, this refers to a pro­gram­ming struc­ture in which we can order data of the same type and use them to solve algorithms.

We can mod­el math­e­mat­i­cal vec­tors using arrays, how­ev­er arrays can con­tain strings of text for example.

Mathematical Vectors in Unity

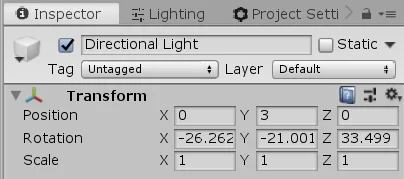
In Uni­ty there are sev­er­al com­po­nents that use vec­tors, the sim­plest of which is the Trans­form com­po­nent that deter­mines the posi­tion, rota­tion and scale of a GameOb­ject in Unity.

For this it uses three three-dimen­sion­al vec­tors. In fig­ure 4 we can see these vec­tors in the inspec­tor. Uni­ty gives the vec­tor com­po­nents the name x, y and z.

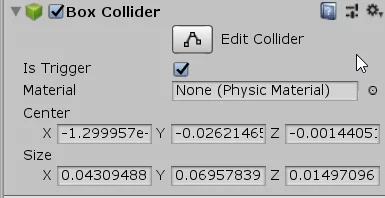
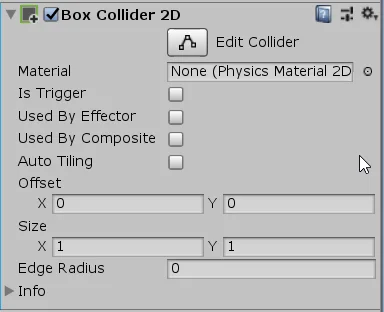
Oth­er com­po­nents such as Col­lid­ers use vec­tors to draw the Col­lid­er, define its posi­tion and size. In fig­ure 5 we see an exam­ple of Col­lid­er in three dimen­sions in which three com­po­nent vec­tors are used and in fig­ure 6 an exam­ple of Col­lid­er 2D in which two com­po­nent vec­tors are used.

In addi­tion to the Uni­ty com­po­nents, in our Script we can cre­ate vec­tors to use in our algorithms. 

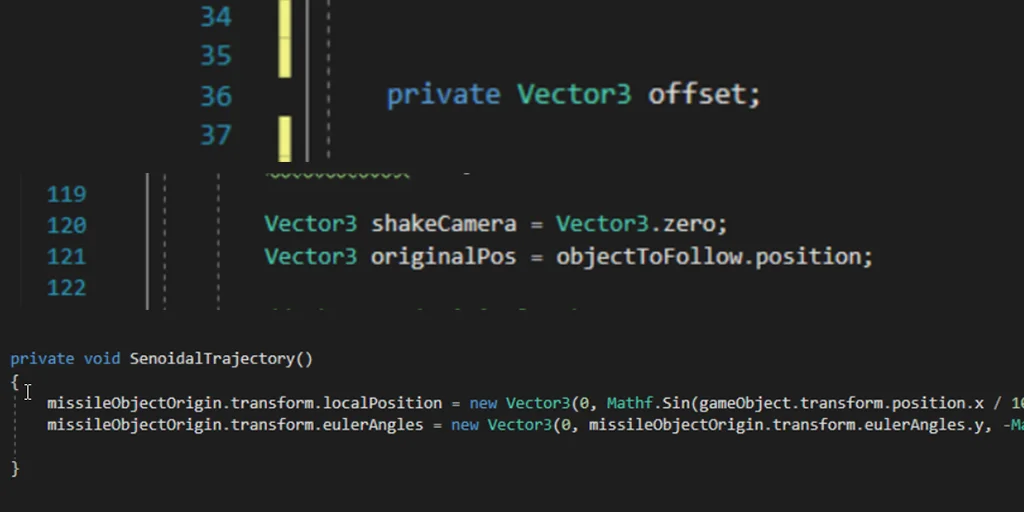
The name of the object by which we refer to these vec­tors in a C# Script for Uni­ty is Vector2 and Vector3. We can see some exam­ples in fig­ure 7.

Conclusion

Vec­tors in math­e­mat­ics are a use­ful tool for rep­re­sent­ing tra­jec­to­ries and forces.

A vec­tor has a mod­ule that deter­mines its size, a direc­tion that deter­mines its ori­en­ta­tion in space, and a sense with­in that direction.

Giv­en a vec­tor we can find a sin­gle line that con­tains it.