Introducción
En este artículo vamos a ver cómo se define la operación factorial de un número, cálculos y propiedades. Se trata de una operación útil que se aplica comúnmente en el desarrollo en serie de funciones.
Definición del Factorial de un Número
Esta operación se simboliza con el símbolo de admiración por delante del número a aplicarla, el factorial de 3 se simboliza !3.
Se aplica a los números naturales incluyendo el 0. Esto quiere decir que no podemos calcularle el factorial a un número negativo o a un número con decimales, ver conjuntos numéricos para más información.
El factorial de 0 es igual a 1, esto es !0 = 1.
El factorial es igual a ese número multiplicado por el factorial del número anterior. Esta propiedad la podemos seguir aplicando hasta llegar al factorial de 0.
Podemos representar esta operación usando el símbolo de productoria, de la siguiente manera:
(1) 
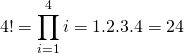
Una forma de calcular el factorial en programación es usando esta notación de productoria y resolverla en un bucle, tal como vimos en el artículo sobre sumatoria y productoria.
Ejemplos de utilización del factorial
Desarrollos en serie
Un ejemplo de utilización de esta operación es en el desarrollo en Serie de Taylor o de potencias, la cual consiste en una serie de términos infinitos a los que podemos ajustar los coeficientes para que se aproximen a una función que queramos y que cumpla las condiciones mínimas para que esto sea posible.
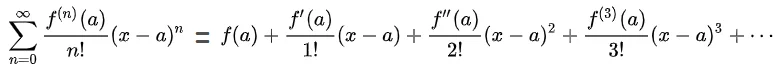
Observen en la figura 1 en el divisor del término de la sumatoria hay un número que va desde 0 a infinito y se le aplica el factorial.
La aproximación por series es algo muy útil porque permite encontrar soluciones numéricas a determinados problemas, en lugar de evaluar una función complicada o incluso una función no conocida, evaluamos polinomios.
Números Combinatorios
Los números combinatorios resultan útiles para varias aplicaciones, por ejemplo para saber cuántas combinaciones posibles existen entre ciertas cantidades. En la definición de números combinatorios se utilizan factoriales:
![\[\binom{n}{m} = \frac{n!}{m!(n-m)!}\]](https://gamedevtraum.com/wp-content/ql-cache/quicklatex.com-3dd201ecfcc4341982584f3674602e5f_l3.png "Rendered by QuickLaTeX.com")
Conclusión
Hemos visto la operación factorial que se simboliza con el signo de admiración y se define como una multiplicación de un número por todos los números naturales anteriores a él.
El factorial se aplica a los números naturales incluyendo el 0.
El factorial de 0 es igual a 1, de ahí en adelante, el factorial de un número se define como el producto de todos los números naturales hasta llegar a ese número.
