Introduction

The Carte­sian coor­di­nate sys­tem is named after the philoso­pher and math­e­mati­cian René Descartes, con­sid­ered the cre­ator of ana­lyt­i­cal geometry.

This sys­tem allows us to rep­re­sent points on a line, in the plane and in space using arrays of num­bers. For exam­ple: (1,5), (-3,0), (4,1,-1), etc.

What is a Cartesian plane?

The Carte­sian plane is defined by two straight lines per­pen­dic­u­lar to each oth­er, one hor­i­zon­tal and one ver­ti­cal, these straight lines are known as Carte­sian axes. Using these axes we can iden­ti­fy any point on the plane with a sin­gle ordered pair of numbers.

The hor­i­zon­tal axis is known as the abscis­sa axis and is usu­al­ly the x‑axis. The ver­ti­cal axis is known as the ordi­nate axis and is usu­al­ly the y‑axis.

The point where the abscis­sa and ordi­nate axes are cut is known as coor­di­nate ori­gin or sim­ply ori­gin and is the point (0.0).

The fol­low­ing fig­ure shows a Carte­sian plane with the point (2,1) plotted.

Quadrants of the Cartesian plane

Quad­rants are char­ac­ter­is­tic regions of the plane defined by changes in signs on coor­di­nate axes.

There are four quad­rants, the first is the upper right region and they are list­ed counterclockwise.

As shown in fig­ure 2, quad­rants are defined in the fol­low­ing regions. 

First quad­rant: { x > 0 , y > 0 }

Sec­ond quad­rant: { x < 0 , y > 0 } 

Third quad­rant: { x < 0 , y < 0 } 

Fourth quad­rant: { x > 0 , y < 0 } 

Representation of functions in the Cartesian plane

The Carte­sian plane also serves to rep­re­sent func­tions, i.e. rules that assign each point of the x‑axis to a point of the y‑axis. Fig­ures 3 to 6 show some exam­ples of func­tion graph­ics in the Carte­sian plane.

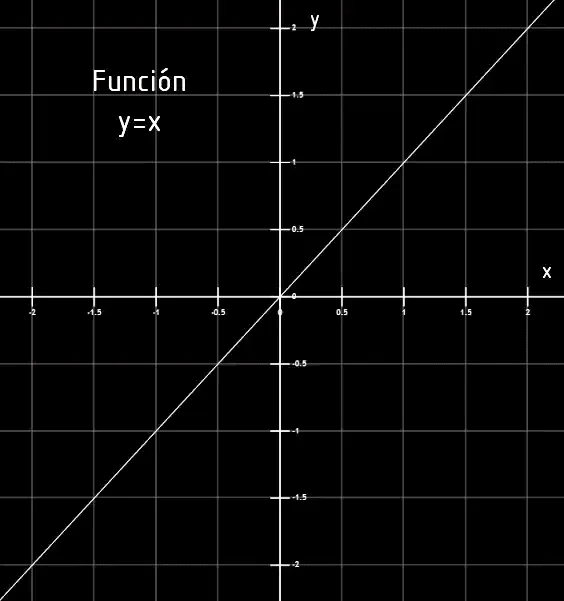
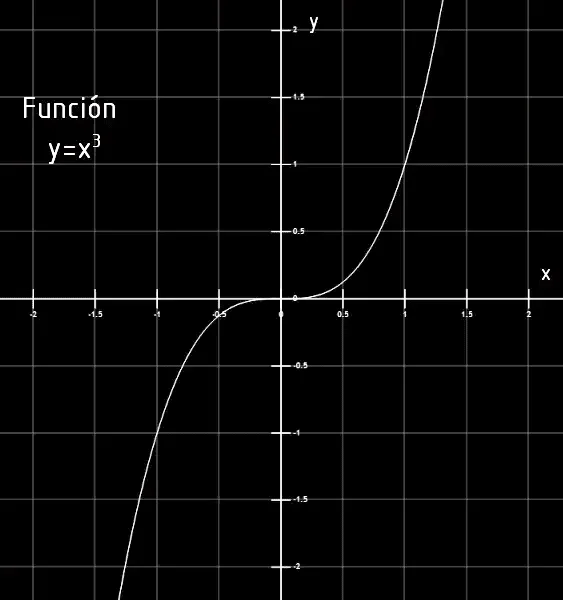
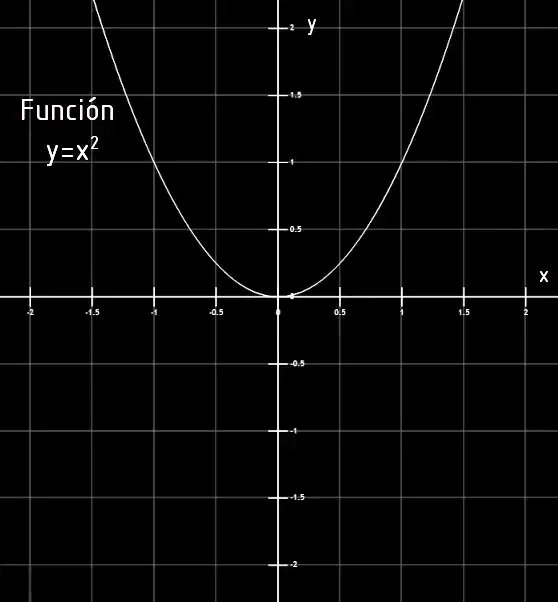
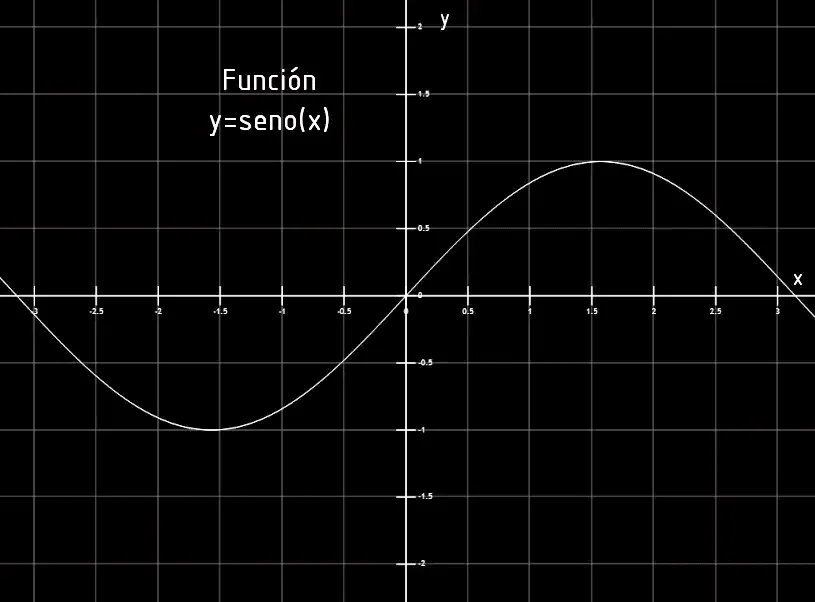
Cartesian system in Unity

Carte­sian coor­di­nates are used in var­i­ous places in Uni­ty, for exam­ple to define the posi­tion of a GameOb­ject in the plane or space. But for the pur­pose I want­ed to make a sim­ple func­tion plot­ter using spheres that move on the x‑axis and their posi­tion on the y‑axis is cal­cu­lat­ed using the expres­sion of the function.

The but­tons allow us to change the expres­sion of the function

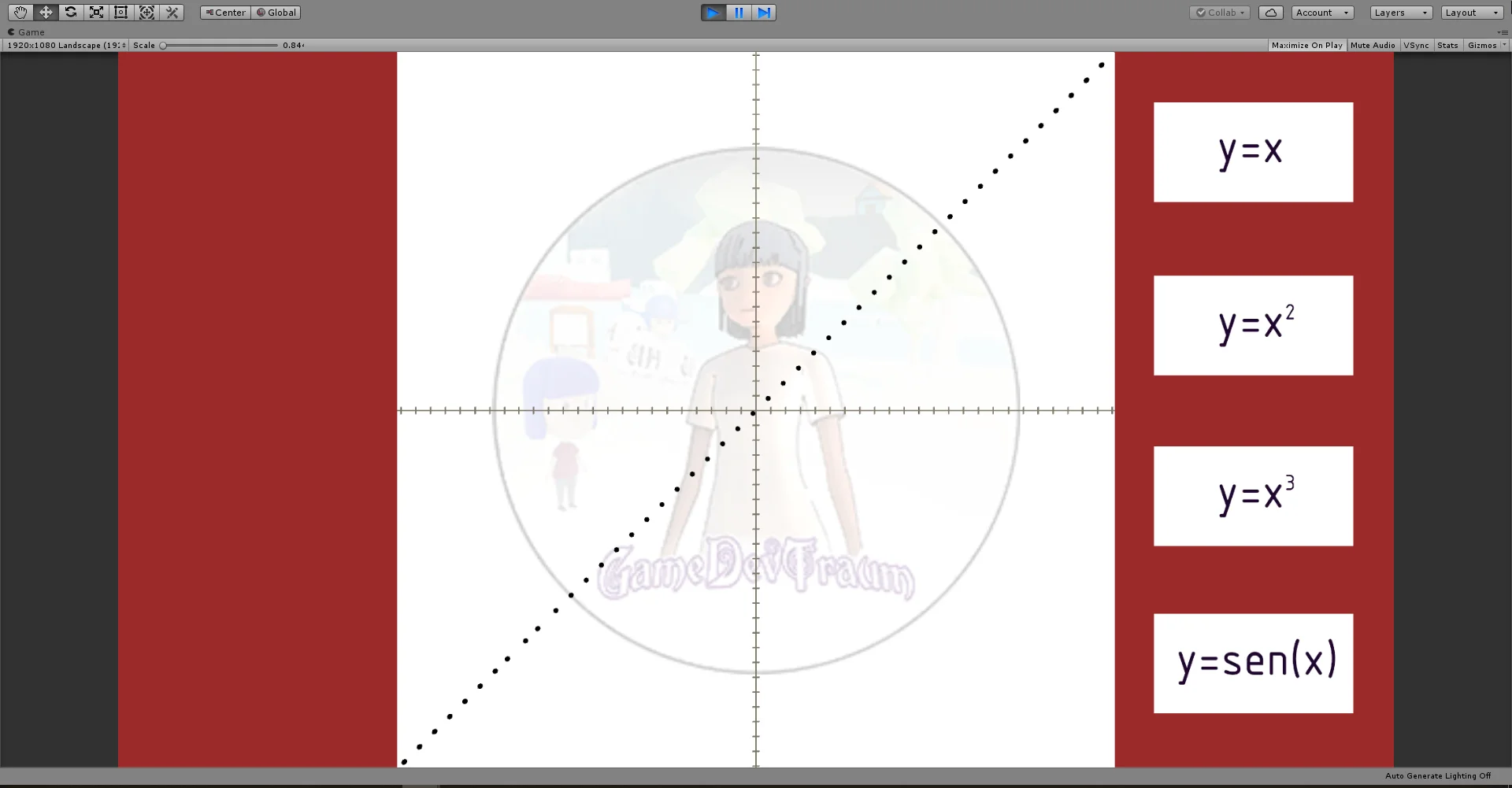
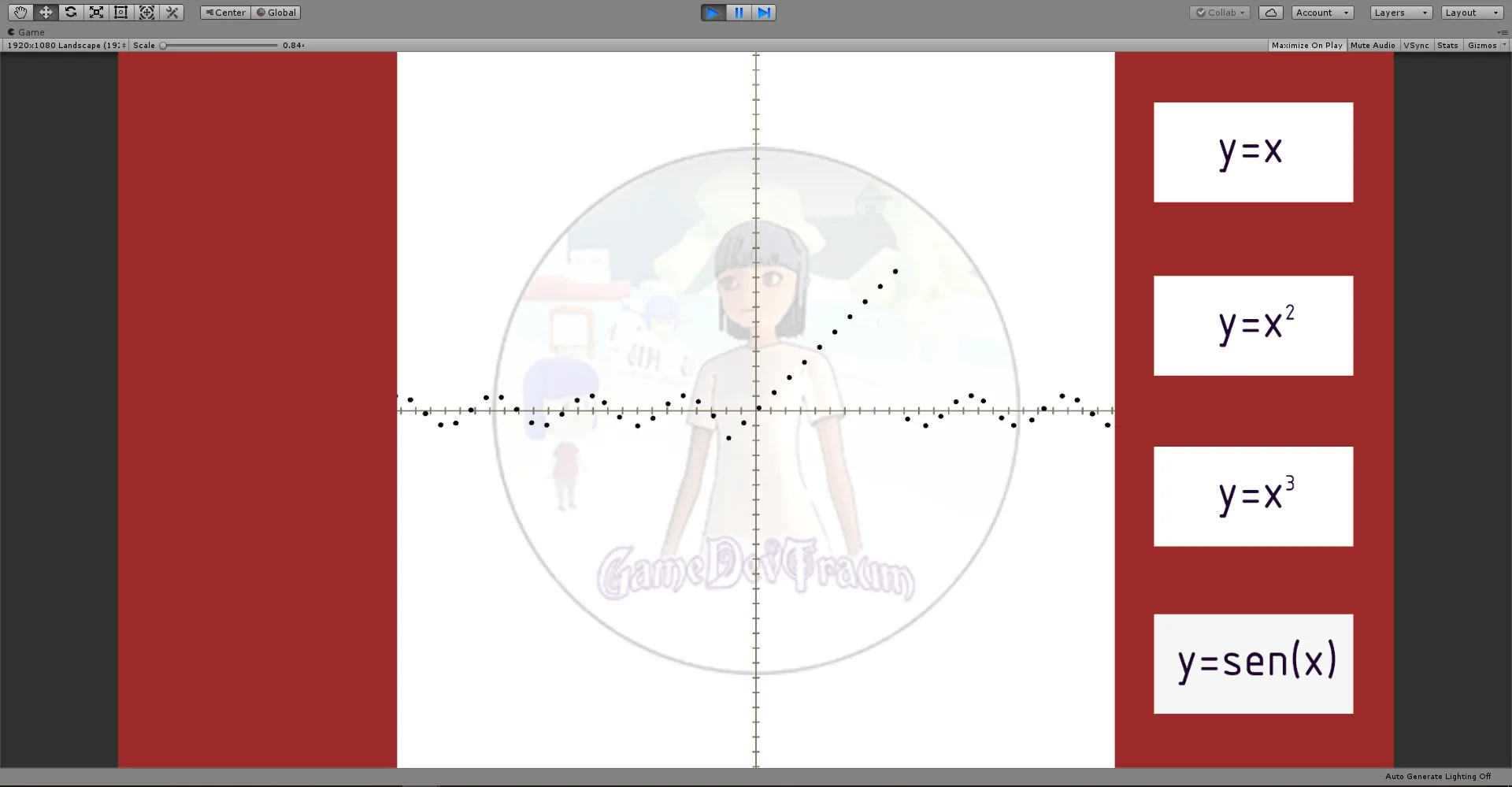
Conclusion

Rec­tan­gu­lar coor­di­nates are often used in Unity.

Under­stand­ing how the Carte­sian plane is used to rep­re­sent points and func­tions in the plane, along with knowl­edge of ana­lyt­i­cal geom­e­try can help us cre­ate new and inter­est­ing solutions.