{ Factorial Function } - Definition, calculations and examples of use.

Introduction

In this article we will see how to define the factorial operation of a number, calculations and properties. It is a useful operation that is commonly applied in the development in series of functions.

Definition of the Factorial Function

This operation is symbolized with the admiration symbol in front of the number to apply it, the factorial of 3 is symbolized !3.

Applies to natural numbers including 0. This means that we cannot calculate the factorial of a negative number or a number with decimals, see numerical sets for more information.

The factorial of 0 is equal to 1, that is !0 = 1.

The factorial is equal to that number multiplied by the factorial of the previous number. We can continue applying this property until we reach the factorial of 0.

We can represent this operation using the product notation, in the following way:

(1) $\begin{equation*} 4! = \prod_{i=1}^{4}{i}= 1.2.3.4 = 24\end{equation*}$

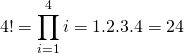
One way to calculate the factorial in programming is to use this producer notation and solve it in a loop, as we saw in the article about summation and product notation.

Examples of use of the factorial

Power Series Expansion

An example of the use of this operation is in the Taylor Series or power series expansion, which consists of a series of infinite terms to which we can adjust the coefficients to approximate a function that we want and that meets the minimum conditions for this to be possible.

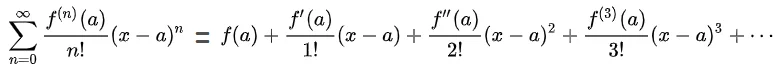
desarrollo en Serie de Taylor de una función f(x). Aplicación del factorial. — Fig. 1: Desarrollo en Serie de Taylor de una función f(x). Aplicación del factorial.

Notice in figure 1 in the divisor of the summation term there is a number ranging from 0 to infinity and the factorial is applied to it.

The series approach is very useful because it allows us to find numerical solutions to certain problems, instead of evaluating a complicated function or even an unknown function, we evaluate polynomials.

Combination

The combination is useful for various applications, for example to find out how many possible combinations exist between certain quantities. You use factorials in the definition of combinatorial numbers:

$\binom{n}{m} = \frac{n!}{m!(n-m)!}$

Conclusion

We have seen the factorial operation that is symbolized with the exclamation point and is defined as a multiplication of a number by all the natural numbers before it.

The factorial applies to natural numbers including 0.

The factorial of 0 is equal to 1, henceforth, the factorial of a number is defined as the product of all natural numbers up to that number.