Introducción
En este artículo vamos a las operaciones de sumatoria y productoria, las cuales nos permiten realizar sumas y productos de manera repetitiva con un patrón conocido, vamos a ver cómo se representan y cómo realizar los cálculos. Al final vamos a ver cómo programar sumatorias y productorias en lenguaje Java o C#.
¿Qué es la sumatoria y la productoria?
La sumatoria y productoria son formas de definir operaciones matemáticas que consisten en secuencias de sumas y productos respectivamente.
Imaginemos que tenemos que sumar o multiplicar todos los números comenzando en el 1 y terminando en el 1000, pero además multiplicar cada uno de ellos por 3.
Utilizando la simbología de la sumatoria y productoria podemos escribir largas operaciones como esas de forma abreviada. Además las propiedades nos pueden ayudar a simplificar la expresión y calcular los resultados con mayor facilidad.
Símbolo de Sumatoria y Desarrollo matemático
La sumatoria se simboliza con la letra griega Sigma en mayúscula.
Debajo del símbolo de sumatoria se indica la variable índice y desde qué valor inicia. En la parte superior del símbolo se indica el último valor que tomará el índice.
A la derecha del símbolo está la expresión que determina todos los términos de la sumatoria, cada término surge de reemplazar el índice en la expresión desde el primer al último valor.
En la ecuación 1 vemos del lado izquierdo la expresión de la sumatoria y del lado derecho la operación desarrollada.
(1) 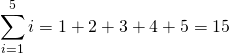
¿Cómo programar una Sumatoria?
Implementar la sumatoria en algún lenguaje de programación es relativamente simple, debemos definir una variable para acumular la suma que debe estar inicializada en 0 (elemento neutro para la suma). Tenemos que tener en cuenta a qué conjunto numérico pertenecen los sumandos, de esto dependerá el tipo de variable a elegir.
Definimos una variable entera para el fin de la sumatoria.
Hacemos un bucle for que va desde el inicio de la sumatoria hasta el final y en el interior del bucle definimos la operación a realizar.
En la figura 1 vemos la implementación de la sumatoria de la ecuación 1 junto con el resultado impreso en consola.

Símbolo de Productoria y desarrollo
La productoria se simboliza con la letra Pi en mayúscula.
Debajo del símbolo de productoria se indica la variable índice y desde qué valor inicia. En la parte superior del símbolo se indica el último valor que tomará el índice.
A la derecha del símbolo está la expresión que determina todos los términos de la productoria, cada término surge de reemplazar el índice en la expresión desde el primer al último valor.
En la ecuación 2 vemos del lado izquierdo la expresión de la productoria y del lado derecho la operación desarrollada.
(2) 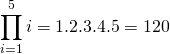
Implementar la productoria en programación
Implementar la productoria es similar a hacer la sumatoria, debemos definir una variable para acumular el producto que deberá estar inicializada en 1 (elemento neutro del producto). También analizamos el tipo de números que estamos multiplicando para elegir el tipo de la variable de acumulación.
Definimos una variable entera para el fin de la productoria.
Hacemos un bucle for que va desde el inicio de la productoria hasta el final y en el interior del bucle definimos la operación a realizar.
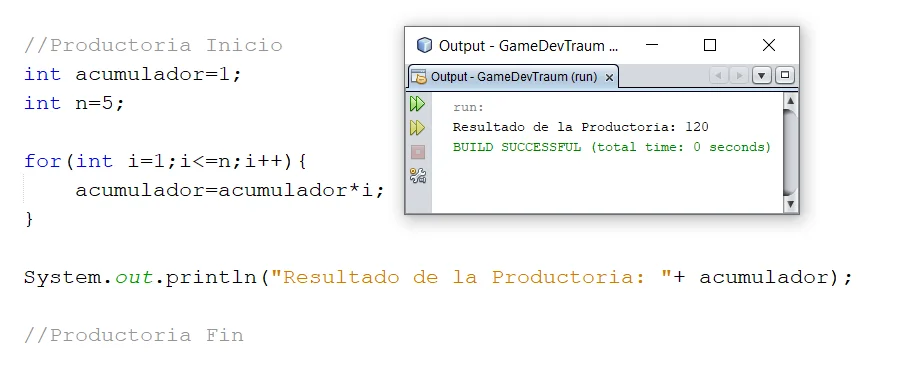
En la figura 2 vemos la implementación de la productoria de la ecuación 2 junto con el resultado impreso en consola.
Vídeo tutorial sobre cómo implementar una sumatoria en lenguaje C#
En el siguiente vídeo explico qué es una SUMATORIA y cómo implementarla en programación
