Introducción

En este artícu­lo vamos a deducir la expre­sión de una rec­ta que pasa por dos pun­tos dis­tin­tos del plano cartesiano.

Existe una úni­ca rec­ta que pasa por dos pun­tos dis­tin­tos dados.

Te recomien­do leer el artícu­lo sobre fun­ciones lin­eales para saber más sobre como rep­re­sen­tar rec­tas en el plano cartesiano.

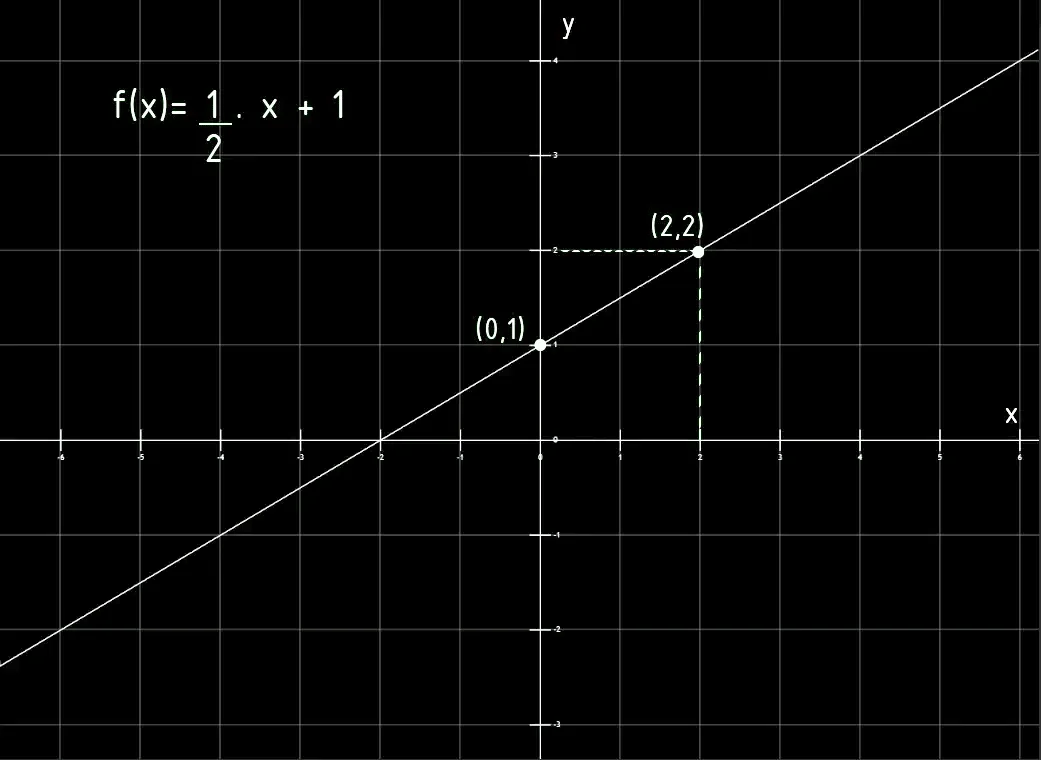
Rectas simples de analizar

Antes de pasar a la deduc­ción de la rec­ta que pasa por dos pun­tos, vamos a ver algunos casos en los que podemos fácil­mente decir de qué rec­ta se tra­ta, sim­ple­mente anal­izan­do los pun­tos que nos dan.

Recta Horizontal

Una rec­ta hor­i­zon­tal es una rec­ta para­lela al eje X del plano carte­siano, osea que todo val­or de X ten­drá como ima­gen un mis­mo val­or de Y.

Dados dos pun­tos podemos darnos cuen­ta de que se tra­ta de una rec­ta hor­i­zon­tal porque los val­ores Y son los mis­mos para ambos pun­tos, por ejem­p­lo P1: (-3,4) y P2: (2,4). En este caso se tra­ta de la rec­ta Y = 4.

La expre­sión genéri­ca de esta rec­ta es:

Y = b

Sien­do b el val­or del eje Y por el que pasa la recta.

Como vemos en la expre­sión, la vari­able inde­pen­di­ente no tiene ningu­na inci­den­cia en la fun­ción, sin impor­tar cuál sea el val­or de X, la fun­ción siem­pre ten­drá el mis­mo val­or para Y.

Recta Vertical

Se tra­ta de una rec­ta para­lela al eje Y del plano cartesiano.

Dados dos pun­tos, podemos darnos cuen­ta de que se tra­ta de una rec­ta ver­ti­cal porque los val­ores de X son los mis­mos para ambos pun­tos, por ejem­p­lo P1: (1,-1) y P2: (1,4).

Para rep­re­sen­tar esta rec­ta podemos decir que se tra­ta de la recta:

X = c

Sien­do c el val­or por donde pasa la rec­ta vertical.

Hay que ten­er en cuen­ta que una rec­ta ver­ti­cal no es una fun­ción lin­eal, ya que las fun­ciones matemáti­cas requieren que para cada val­or de la vari­able inde­pen­di­ente (en este caso la vari­able x), exista un úni­co val­or para la fun­ción. En una rec­ta ver­ti­cal ten­emos infini­tos val­ores dis­tin­tos para un úni­co val­or de X.

Recta identidad

La rec­ta iden­ti­dad es una rec­ta incli­na­da a 45 gra­dos que pasa por el ori­gen y es car­ac­terís­ti­ca porque para cualquier val­or de la vari­able inde­pen­di­ente X, la vari­able depen­di­ente Y vale lo mis­mo. Es decir que si tomamos X = 2, el val­or de Y tam­bién es 2.

La expre­sión de esta rec­ta es:

Y = X

Entonces si por ejem­p­lo nos dan los pun­tos P1: (-2,-2) y P2: (3,3), como vemos que para ambos pun­tos los val­ores de X y de Y coin­ci­den, podemos fácil­mente deter­mi­nar que se tra­ta de la rec­ta identidad.

Recta identidad invertida

En este caso se tra­ta de una rec­ta sim­i­lar a la rec­ta iden­ti­dad, solo que el val­or de Y es el opuesto de X, por ejem­p­los si ten­emos los pun­tos P1: (-2,2) y P2: (3,-3) , podemos deter­mi­nar fácil­mente que se tra­ta de esta recta.

La expre­sión de esta rec­ta es:

Y = — X

Deducción de la recta que pasa por dos puntos

Aho­ra vamos a deducir la expre­sión de una rec­ta que pasa por dos pun­tos a par­tir de una rec­ta genéri­ca. Como se vio en el artícu­lo de fun­ción lin­eal, una rec­ta cualquiera se puede expre­sar como:

(1)  

donde a es la pen­di­ente y b es la orde­na­da al ori­gen de la función.

Vamos a con­sid­er­ar que ten­emos dos pun­tos genéri­cos P1: (x1 , y1) y P2: (x2 , y2). Como quer­e­mos que ambos pun­tos pertenez­can a la rec­ta, nece­sari­a­mente tienen que sat­is­fac­er la expre­sión de la fun­ción lin­eal, por lo tan­to podemos escribir dos ecuaciones:

(2)  

(3)  

Podemos plantear un sis­tema de dos ecua­ciones en el que las dos incóg­ni­tas son a y b. Así que por ejem­p­lo podemos tomar la ecuación 2 y despe­jar la incóg­ni­ta b:

(4)  

Luego tomamos esta expre­sión y la reem­plazamos en la segun­da ecuación 3:

(5)  

Rea­gru­pan­do y sacan­do fac­tor común con la incóg­ni­ta a tenemos:

(6)  

Final­mente la pen­di­ente de la rec­ta será igual a:

(7)  

En la expre­sión 7 podemos ver que si los val­ores de X de ambos pun­tos coin­ci­den (es decir el caso de la rec­ta ver­ti­cal), el denom­i­nador vale 0 y la expre­sión resul­ta inde­ter­mi­na­da, impidién­donos encon­trar un val­or para la pendiente.

Una vez que ten­emos el val­or de la pen­di­ente, podemos reem­plazar­lo en en cualquiera de las ecua­ciones del sis­tema para encon­trar el val­or de b.

(8)  

Despe­jan­do:

(9)  

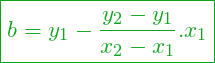
Con esto encon­tramos de man­era genéri­ca cuán­to valen los coe­fi­cientes a y b de una rec­ta que pasa por dos pun­tos cualquiera del plano:

(10)  

(11)  

Aho­ra sim­ple­mente reem­plazamos los val­ores por los pun­tos dados y ten­emos la expre­sión de la rec­ta que pasa por dos pun­tos en particular.

Verificación de los resultados

La ver­i­fi­cación de la solu­ción es la her­ramien­ta que tienes para saber si te has cometi­do un error en algu­na cuen­ta, una vez que tienes la expre­sión de la rec­ta, no olvides reem­plazar en la ecuación de la rec­ta los pun­tos por los que la rec­ta tiene que pasar, esto se hace para ver­i­ficar que ambos pun­tos sat­is­facen la ecuación, si esto no ocurre, has cometi­do un error en algún paso de la deducción.