Introducción
En este artículo vamos a ver qué es una función cuadrática, su expresión matemática, sus características, cómo graficarla en el plano cartesiano y para qué nos puede ser útil en el desarrollo de juegos con ejemplos en Unity.
Expresión matemática de una función cuadrática
La expresión polinómica de una función cuadrática es:

Se lee comunmente «f de x», siendo X la variable independiente, a, b y c números reales constantes.
Características de una función cuadrática
Dominio
El dominio es el intervalo de valores admisibles para la variable independiente, comunmente denominada X.
En el caso de la función cuadrática el dominio es el conjunto de los números reales.
En otras palabras podemos elegir cualquier valor de X perteneciente al conjunto de los números reales y encontraremos su valor f (X) correspondiente.
Haz clic aquí para leer el artículo sobre conjuntos numéricos.
Gráfica en el plano cartesiano de una función cuadrática
La gráfica de f (X) en el plano cartesiano es una parábola. Puedes graficar una función cuadrática a partir de una tabla de valores, aquí tienes un ejemplo del procedimiento.
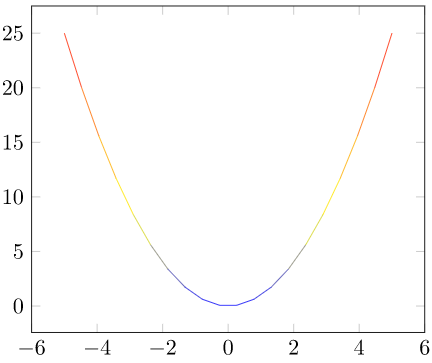
Fig. 1: Gráfica de una función cuadrática con el coeficiente a positivo.

Fig. 2: Gráfica de una función cuadrática con el coeficiente a negativo.
Si te interesa puedes leer un poco más sobre el sistema cartesiano en este artículo.
Raíces de la función
Las raíces de una función cuadrática son los valores de x para los cuales f (x) vale 0, es decir los puntos en los que la función toca al eje de las abscisas (comunmente el eje x).
Se pueden dar tres casos, la función tiene una raíz, es decir hay un único valor de x para el cuál la función vale 0.
La función puede tener dos raíces, es decir hay dos valores distintos de x para los cuales la función vale 0.
La función puede no tener raíces en el conjunto de los números reales pero si en el de los números complejos.
Para calcular las raíces de una función cuadrática usamos una fórmula que se conoce comunmente como fórmula de Bhaskara
Dada la siguiente ecuación:

Los dos valores de x que satisfacen esta ecuación están dados por:

El signo más menos ( ± ) quiere decir que son dos ecuaciones, en una usamos el signo más y obtenemos X1 y en otra usamos el signo menos y obtenemos X2.
Como observación, si lo que está dentro de la raíz cuadrada dá como resultado un número negativo quiere decir que la ecuación no tiene solución en el conjunto de los reales, en este caso gráficamente vemos que la parábola no corta el eje de las abscisas.
Algunos ejemplos en Unity de función cuadrática
Dibujar trayectorias parabólicas
Podríamos estar interesados en dibujar a través de código trayectorias con forma de parábolas, por ejemplo para sistemas de partículas, o para representar el posible trayecto que un proyectil pueda seguir al lanzarlo.
En el siguiente video muestro cómo un conjunto de GameObjects siguen una trayectoria parabólica descrita por dos funciones cuadráticas a las que se pueden ajustar los parámetros.
Observación 1: las esferas del mismo color siguen la trayectoria definida por la misma ecuación solo que para una tomo la constante a como positiva y en la otra como negativa, por esta razón se reflejan respecto a los ejes.
Observación 2: Noten que al comienzo y al final del video el valor de a es 0, esto significa que se anula el término cuadrático y nos quedamos con una función lineal.
Implementar magnitudes cuadráticas
En la física existen muchas magnitudes cuadráticas que podríamos estar interesados en implementar en nuestro juego.
Un ejemplo de esto puede ser el movimiento con aceleración constante, es decir objetos que se mueven con velocidad que cambia de manera lineal. Por ejemplo cuerpos en caída libre por acción de la gravedad o vehículos que aceleran.
Algunos tipos de energía como la energía cinética o la energía potencial elástica son proporcionales al cuadrado de una magnitud.
Conclusión
La función cuadrática es una función polinómica de orden 2 cuya gráfica en el plano cartesiano es una parábola.
Las raíces de la función cuadrática son los valores de x en los que se cumple que f (x) = 0. Podemos utilizar la fórmula de Bhaskara para encontrarlas.
Una función cuadrática puede tener dos raíces distintas, una raiz o no tener raíces en el conjunto de los números reales. Si una función cuadrática no tiene raíces reales, gráficamente no intersecta el eje de abscisas.
Hay magnitudes físicas así como también trayectorias de cuerpos acelerados que pueden describirse por funciones cuadráticas, por eso es útil tener conocimiento sobre sus características y así poder implementarlas correctamente en Unity.
