Qué es una MATRIZ en Matemática - Definición y Ejemplos

Introducción

En este artículo vamos a ver qué es una matriz en matemática, cómo se define, qué tipos de matrices hay y vamos a ver ejemplos de matrices.

Una matriz es un arreglo de números ordenado, que consiste en una serie de filas y columnas, de modo que cada elemento ocupa una posición y puede ser identificado por su número de fila y de columna.

Dadas dos matrices podremos realizar ciertas operaciones entre ellas siempre que cumplan determinadas condiciones.

Una de las aplicaciones mas útiles de las matrices es la resolución de sistemas de ecuaciones. Por ejemplo, si tenemos un sistema de dos ecuaciones con dos incógnitas, podemos representar este sistema con una matriz cuadrada de 2×2 (llamémosla A), multiplicada por un vector columna de incógnitas (vector x) y ese producto igualarlo al vector columna de términos independientes (digamos B). Este sistema se representaría de la siguiente manera:

A.x = B

Lo cual recuerda mucho a una ecuación lineal simple en la que tenemos una incógnita (x) que está multiplicada por un coeficiente (A) y esto es igual a un valor (B), para resolver esa ecuación lineal basta con dividir a ambos miembros por el coeficiente A y de esta forma despejaríamos la incógnita x. No se puede hacer divisiones con matrices pero se puede recurrir a una operación análoga que es multiplicar ambos miembros por la matriz inversa de A (siempre que exista la matriz inversa de A), con esto se despeja el vector incógnita.

x = A^-1.B

Definición de una Matriz en Matemática

Una matriz la representamos con una letra del alfabeto en mayúscula (por ejemplo A, B, C…), luego podemos explicitar sus elementos, para ello vamos a escribir sus números en una tabla que contendrá una determinada cantidad de filas y columnas.

En la figura 1 vemos un ejemplo de una matriz genérica A de m filas y n columnas, vemos que en la derecha de la igualdad se ha explicitado la matriz escribiendo sus elementos a_ij.

una matriz A genérica de m filas y n columnas en la que se explicitan sus elementos aij — Fig. 1: Matriz A genérica de m filas y n columnas, a la derecha se muestran sus elementos a_ij.

La matriz de la figura 1 hace referencia a una matriz cualquiera, se suele utilizar para las definiciones y propiedades de las matrices.

Ejemplos de matrices con valores

Vamos a ver ejemplos de matrices que tienen características particulares ya sea por su tamaño o por la forma en la que están distruibuidos sus elementos.

Matriz Cuadrada

Una matriz cuadrada es una matriz en la que el número de filas coincide con el número de columnas. En la figura 2 vemos un ejemplo de una matriz B de 3 filas y 3 columnas.

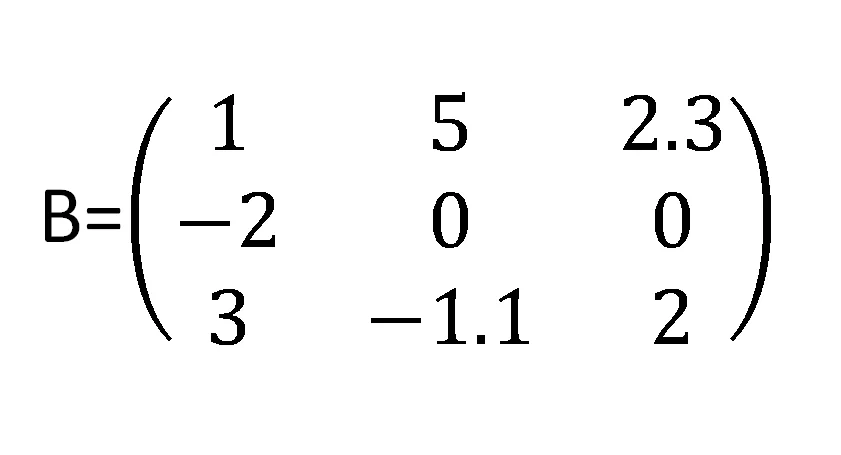
matriz B de 3 filas y 3 columnas en la que se explicitan sus elementos bij — Fig. 2: Ejemplo de una matriz B de 3 filas y 3 columnas, a la derecha se muestran sus elementos b_ij.

En una matriz cuadrada tenemos una diagonal principal que son los elementos b_ij para los cuales i=j, en el caso de la figura 2 son los elementos b₁₁, b₂₂ y b₃₃ cuyos valores son 1, 0 y 2 respectivamente.

La diagonal principal divide a la matriz en dos partes, un triángulo superior y un triángulo inferior.

Matriz Diagonal

Una matriz diagonal es una matriz en la que todos sus elementos no nulos están ubicados en la diagonal principal y el resto de los elementos son 0. En las figuras 3 y 4 vemos ejemplos de matrices diagonal, en particular la matriz de la figura 4 se la conoce como matriz identidad.

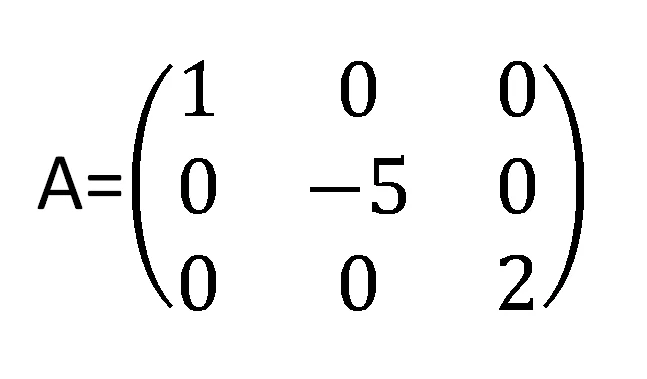
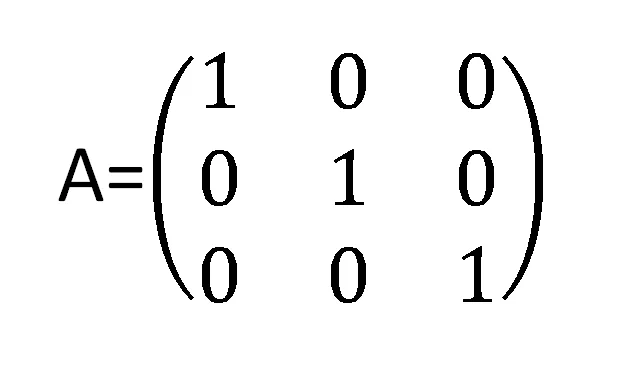
identidad de 3x3, todos sus elementos no nulos están en la diagonal principal y valen 1 — Fig. 4: Matriz identidad de 3×3.

Matriz Triangular

Una matriz triangular es una matriz que tiene todos sus elementos no nulos de un lado de la diagonal principal y el resto de los elementos son 0. Podemos tener matrices triangular superior y matrices triangular inferior, como se observa en las figuras 5 y 6 respectivamente.

ejemplo de una matriz triangular inferior de 3x3, todos sus elementos no nulos están en la diagonal principal y por debajo — Fig. 6: Ejemplo de una matriz A de 3×3 triangular inferior.

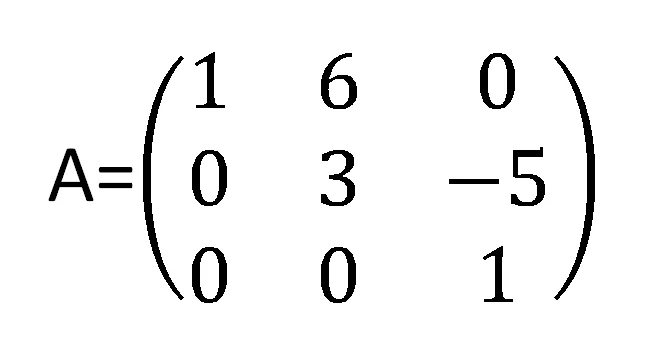
Conclusión

Una matriz en matemática es una arreglo de números ordenados en una cantidad fija de filas y columnas.

Las matrices cuadradas son las matrices en las que el número de fila coincide con el número de columnas. En una matriz cuadrada tenemos una diagonal principal que es el elemento en el cual el número de fila coincide con el número de columna.

Una matriz diagonal es una matriz cuadrada en la que todos sus elementos no nulos se encuentran en la diagonal principal. Particularmente la matriz identidad es una matriz diagonal en la que todos los elementos valen 1.

Las matrices triangulares son aquellas en la que todos los elementos no nulos se encuentran en la diagonal principal y por encima o por debajo, de aquí las podemos clasificar en matriz triangular superior o inferior.

Matrices en Matemática – Definición y Ejemplos