Introducción
En entradas anterior vimos cómo definir matrices en programación y cargarle datos, en este artículo veremos cómo multiplicar dos matrices utilizando arreglos bidimensionales.
Datos iniciales
Partiremos de dos matrices A y B con sus datos precargados y analizaremos un método que realizará la suma de dos matrices que se envíen como parámetro y devuelve la matriz resultado, para más detalles sobre métodos en programación, sintaxis y parámetros de entrada y salida consultar este vídeo.
En la figura 1 vemos la declaración de dos matrices de 2×2 y la carga de sus datos, luego en las líneas 27 y 28 se hacen las llamadas al método que se encarga de multiplicar las matrices que se envíen cómo parámetro y devolver la matriz resultante.

Algoritmo para multiplicar matrices en programación
El producto de matrices no es conmutativo, de modo que importa el orden en el que se multiplican las matrices. Vamos a considerar que la matriz A está a la izquierda y la multiplicaremos por la matriz B que está a la derecha.
El procedimiento para multiplicar dos matrices consiste en multiplicar cada elemento de la i-ésima fila de la matriz de la izquierda por cada elemento de la j-ésima columna de la matriz derecha y luego sumar estos productos, el resultado de esa suma será el elemento ij de la matriz resultante. Por lo tanto para que se pueda llevar a cabo el producto de matrices debe cumplirse la condición que el número de columnas de la matriz de la izquierda debe coincidir con el número de filas de la matriz de la derecha.
El resultado de la multiplicación de las matrices A y B será otra matriz que tendrá un número de filas igual a las filas de A y un número de columnas igual a la cantidad de columnas de B.
Análisis del algoritmo
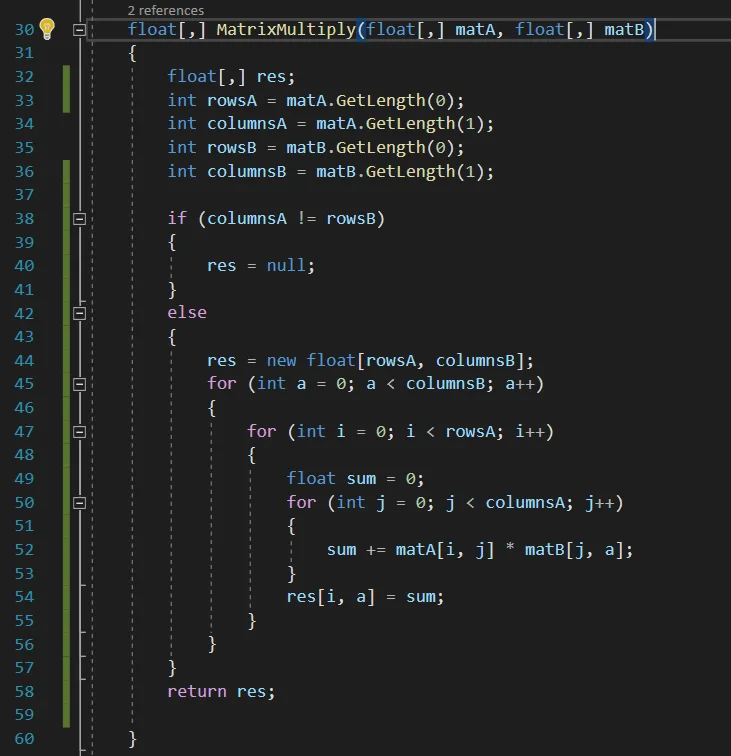
En la figura 2 vemos la implementación de un algoritmo que multiplica dos matrices que se envíen como parámetro. Primero se declara la matriz resultado y se leen los tamaños de ambas matrices, esto se hace en las líneas de la 32 a la 36.
Luego se comprueba si es posible multiplicar ambas matrices, de no ser posible el resultado será null, caso contrario se procede a resolver el producto de matrices.
Se crea la estructura de la matriz resultado con la cantidad de filas y columnas correspondientes (ante la duda ver la descripción más arriba). Luego para determinar el valor de cada elemento resultante se utilizan los tres bucles for anidados que se observan en la figura 2.