Introducción
En este artículo vamos a ver cómo son las funciones seno y coseno, sus expresiones matemática, su gráfica en el plano cartesiano y sus características principales.
Expresión matemática de una función Seno y Coseno
La expresión matemática de la función seno es:
(1) ![]()
La expresión matemática de la función coseno es:
(2) ![]()
Se lee comunmente «f de x», siendo X la variable independiente, a, b, x0 y c números reales constantes.
Características de las funciones Seno y Coseno
Dominio
El dominio es el intervalo de valores admisibles para la variable independiente, comunmente denominada X.
En el caso de las función seno y coseno el dominio es el conjunto de los números reales, es decir la variable independiente puede tomar cualquier valor desde menos infinito a más infinito.
Funciones trigonométricas en el plano cartesiano
La gráfica de f (X) en el plano cartesiano es una onda periódica que se repite en todo el dominio. Puedes graficar las funciones seno y coseno a partir de una tabla de valores.

Fig. 1: Gráfica de una función cuadrática con el coeficiente a positivo.

Fig. 2: Gráfica de una función cuadrática con el coeficiente a negativo.
Desplazamiento de las funciones Seno y Coseno
Hay un valor en el eje «y» respecto del cual las funciones seno y coseno oscilan, si trazamos una línea horizontal en ese valor del eje podemos ver que las funciones se alejan desde ese valor una cierta cantidad hacia arriba, luego vuelven y bajan exactamente la misma cantidad.
El desplazamiento que las funciones Seno y Coseno tienen en el eje y está dado por la constante «c» en las ecuaciones 1 y 2.
En las figuras 1 y 2 el desplazamiento vale 0.
Amplitud de las funciones Seno y Coseno
El término «a» que multiplica a las funciones seno y coseno, en las ecuaciones 1 y 2 se lo conoce como amplitud de la función y es lo que determina la excursión que tendrá la función en el eje y.
Si nos ubicamos en el valor de desplazamiento en el eje y, la función se moverá hacia arriba y abajo una cantidad igual a el valor de a.
Frecuencia de la funciones Seno y Coseno
Las funciones Seno y Coseno son periódicas, esto quiere decir que hay una porción del dominio en el que la función toma valores únicos y luego este patrón se repite en el resto del dominio, infinitamente. Es como si tomáramos ese trozo de la función, lo copiamos y lo pegamos hacia adelante y atrás en el eje x.
Esto quiere decir que podemos definir con qué frecuencia las funciones se repiten. Si la frecuencia es mayor, la función se repetirá más veces en el eje x.
La frecuencia de una función se la suele representar con la letra f y su valor concretamente está dado por el coeficiente b en las ecuaciones 1 y 2.
Período de las funciones Seno y Coseno
El período es la distancia en el eje x que la función recorre desde que comienza hasta que finaliza para luego volver a repetirse.
El período se lo simboliza con la letra T en mayúscula, no está a simple vista en la función pero puede calcularse como 2 veces PI, dividido por el valor de la frecuencia, es decir:
(3) 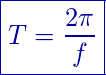
Siendo f la frecuencia de la función, este valor es el coeficiente b en las ecuaciones 1 y 2.
Desfasaje de las funciones Seno y Coseno
El desfasaje es el corrimiento que tiene la función en el eje x, este corrimiento puede ser a la izquierda o a la derecha y está dado por el valor que sumamos o restamos (respectivamente) al valor de b.x, en el argumento de las funciones seno y coseno, he representado este valor como x0.
Relación que existe entre las funciones Seno y Coseno
Si vemos las figuras 1 y 2 vemos que las gráficas de la función seno y coseno son muy similares, de hecho resultan idénticas a simple vista sin examinar los ejes. Esto se debe a que la única diferencia que existe entre ambas es que tienen un desfasaje de 90 grados o medio PI en radianes una de la otra.
Esto quiere decir que utilizando una función seno y aplicándole un desfasaje podemos hacer que sea idéntica al coseno y visceversa. Osea que dada la gráfica de una de estas funciones podemos representarla como seno o como coseno, matemáticamente es igual.
Los valores de las funciones seno y coseno puras, es decir sen(x) y cos(x), los podemos representar utilizando un círculo de radio de 1 centrado en el origen como los catetos de un triángulo rectángulo que se forma con tres puntos. El primer punto es el origen (0,0), el segundo punto es un punto del círculo que estará definido por un segmento que parte desde el origen y tiene determinado ángulo respecto de la parte positiva del eje x; y el tercer punto es la proyección del segundo punto sobre el eje x.
Lo anterior es bastante difícil de imaginar pero podemos verlo ilustrado en el siguiente gif tomado de esta página de Wikipedia.
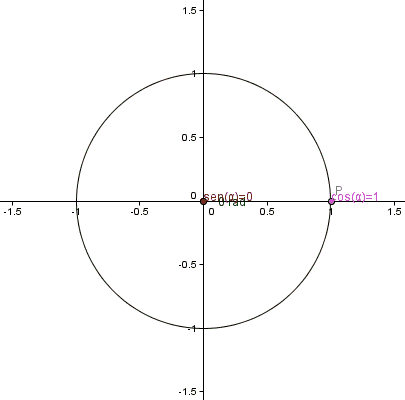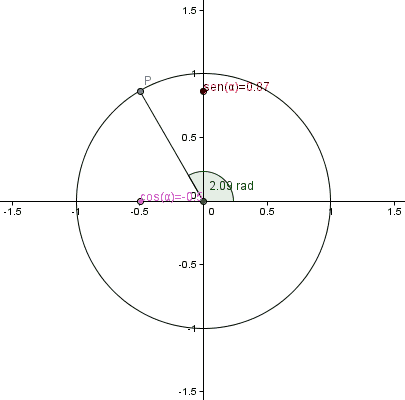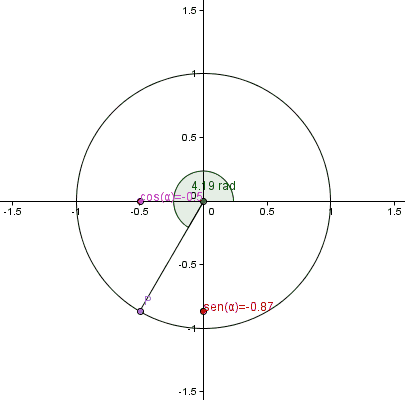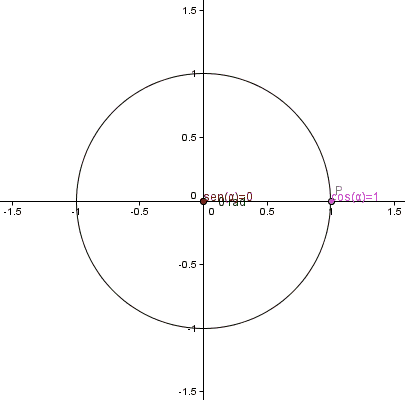
En todo momento vemos que el coseno se corresponde con el cateto del eje x en el triángulo rectángulo y el valor del seno está en el cateto sobre el eje y.
