Introducción
Un divisor de voltaje resistivo es un arreglo de dos resistencias en serie que nos permite tener en el punto medio una fracción del voltaje en los extremos.
Aplicaciones de un divisor resistivo
El divisor con potenciómetro se suele usar como entrada analógica en los variadores de frecuencia de los motores. Utilizando el potenciómetro cambiamos la velocidad del motor.
También se puede polarizar un transistor BJT con un divisor, conectando el punto central de este a la base del transistor.
Principio de funcionamiento del divisor resistivo
En la figura 1 vemos un arreglo que puede ser usado como un divisor.
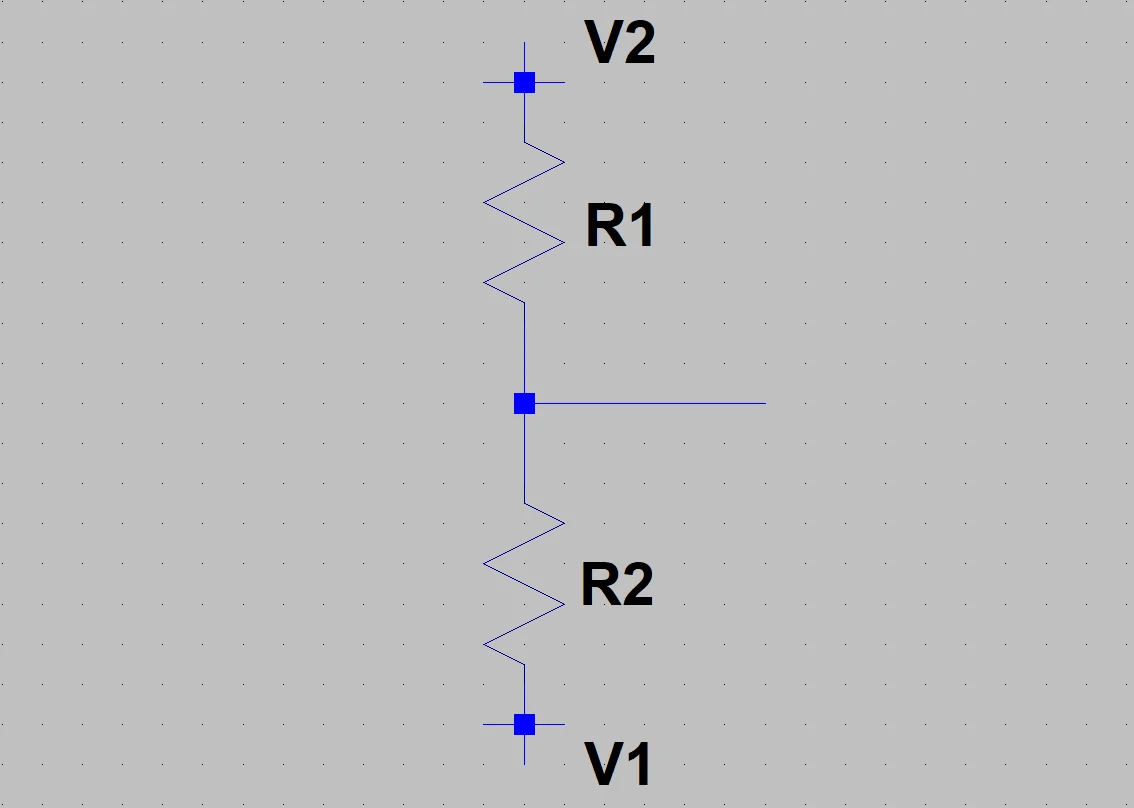
Para entender cómo funciona debemos considerar las caídas de potencial en ambas resistencias.
El voltaje que cae en una resistencia es la corriente que circula por ella multiplicada por el valor resistivo.
Simulación en LT Spice
Para ver cómo funciona un divisor resistivo vamos a hacer una simulación utilizando LT Spice. Si necesitás ayuda para empezar con LT Spice entrá en este artículo donde explico cómo instalarlo y hago un circuito simple para simular.
En el siguiente video puedes ver el proceso de instalación y el diseño y simulación de un circuito con resistencias serie y fuente de voltaje continuo.
Vamos a analizar dos casos, cuando las resistencias son iguales y cuando una es mayor o menor que otra.
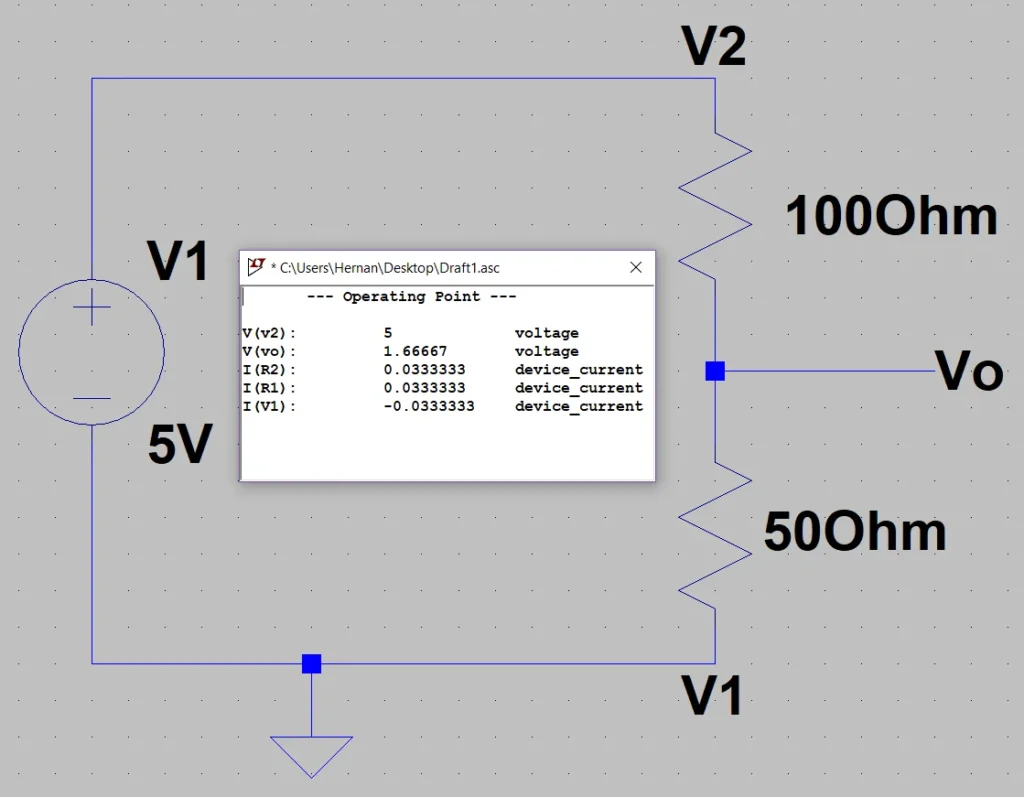
Caso 1: Resistencias iguales
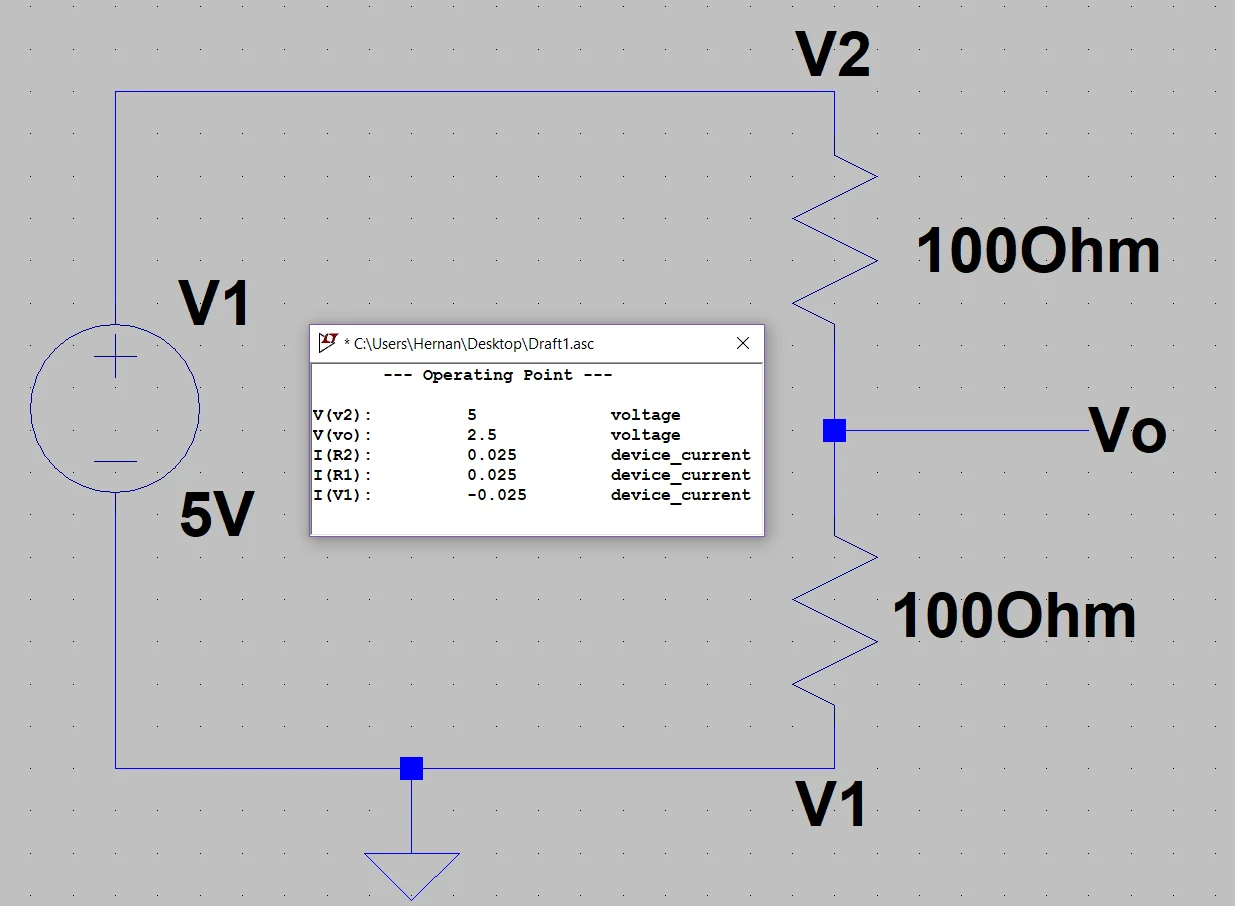
En este caso podemos intuir que la caída de potencial en ambas resistencias será la misma (debido a que circula la misma corriente a través de ellas y su valor resistivo es igual), por lo tanto en el punto medio del divisor tendremos un valor de voltaje igual al valor medio entre la diferencia de potencial en los extremos.
En la figura 2 podemos ver que el voltaje en Vo es 2.5 Volts, la mitad de los 5 Volts aplicados en el divisor.
Con este resultado podemos estar tentados a decir que el voltaje en el punto medio del divisor va a ser igual a la mitad del valor aplicado en V2, pero esto no siempre es así.
Esto sólo se cumple si en V1 tenemos aplicados 0 Volts (en la figura 2 V1 está a tierra).
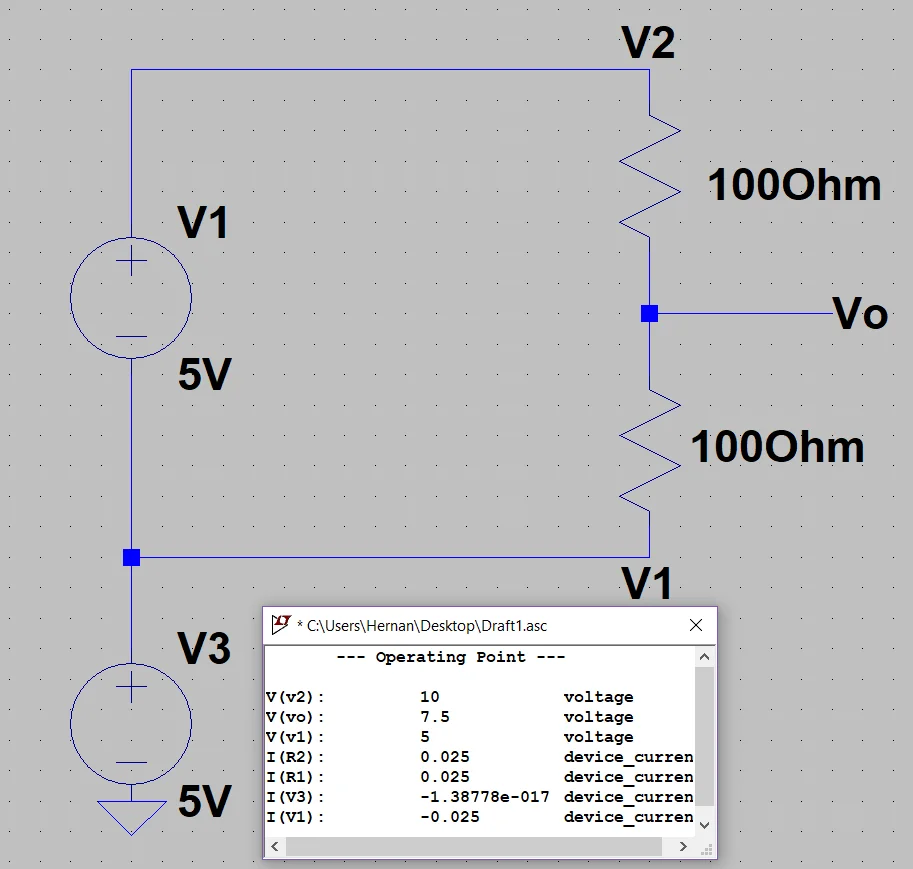
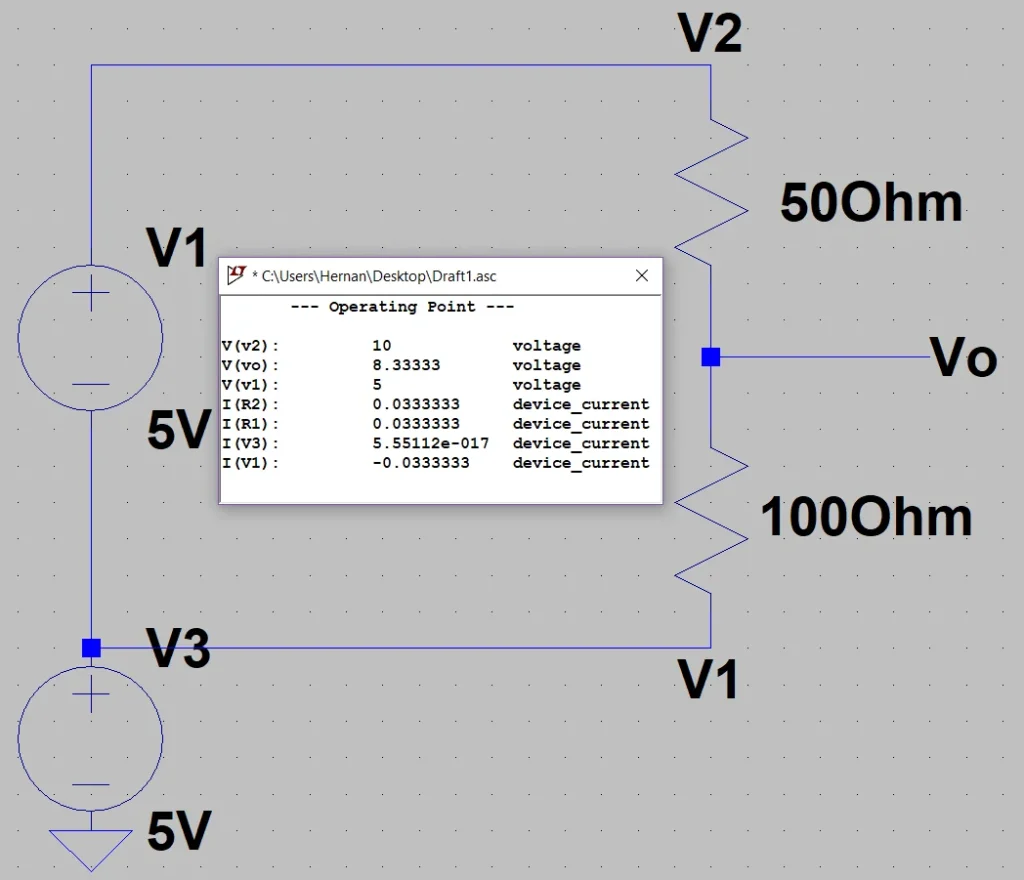
En la figura 3 vemos un ejemplo en el que esto no se cumple, en este caso la diferencia de potencial en el divisor sigue siendo 5 Volts, pero V1 no se encuentra a tierra sino que tiene aplicado 5 Volts mientras que V2 tiene 10 Volts.
El resultado es que en Vo tenemos la mitad de la diferencia de potencial aplicada más el voltaje V1.
Caso 2: Resistencias distintas
En la figura 4 consideramos R1 más pequeña que R2 y en la figura 5 el caso contrario.
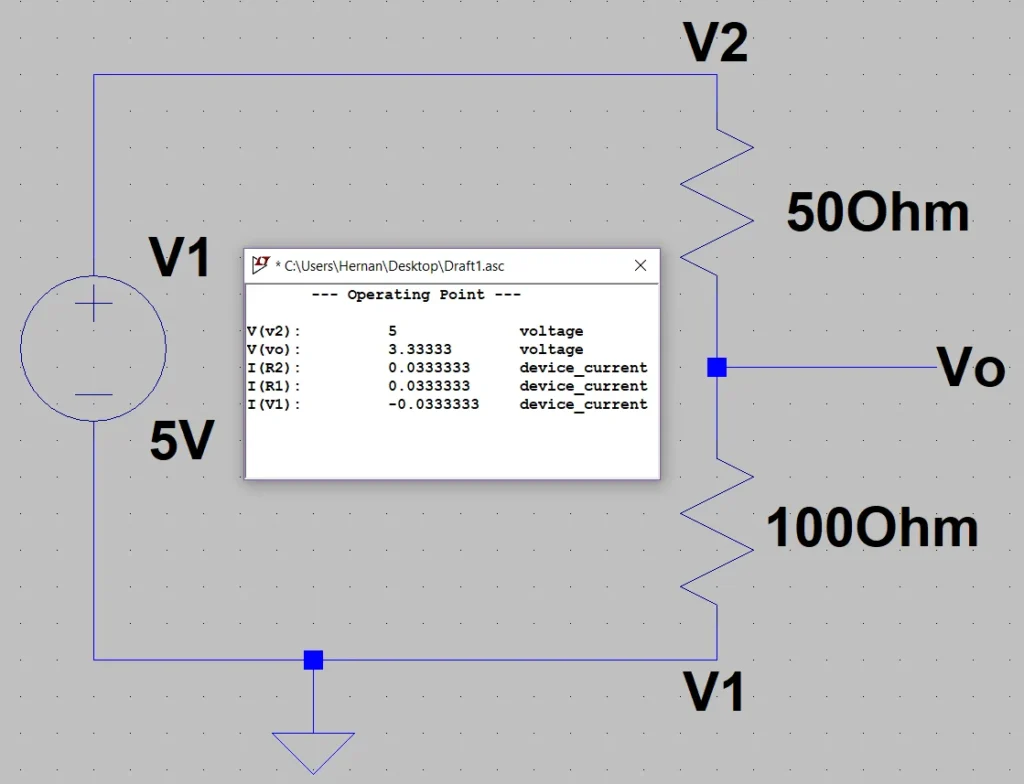
Basándonos en los resultados podemos decir que si el 100% del valor resistivo es 150 Ohms, 50 Ohms y 100 Ohms serán aproximadamente el 33% y 66% respectivamente.
Estos porcentajes parecen verse reflejados en la tensión Vo, ya que en la figura 4 la tensión 3.3 V es aproximadamente el 66% de 5 V mientras que 1.6 V es aproximadamente el 33% de 5V.
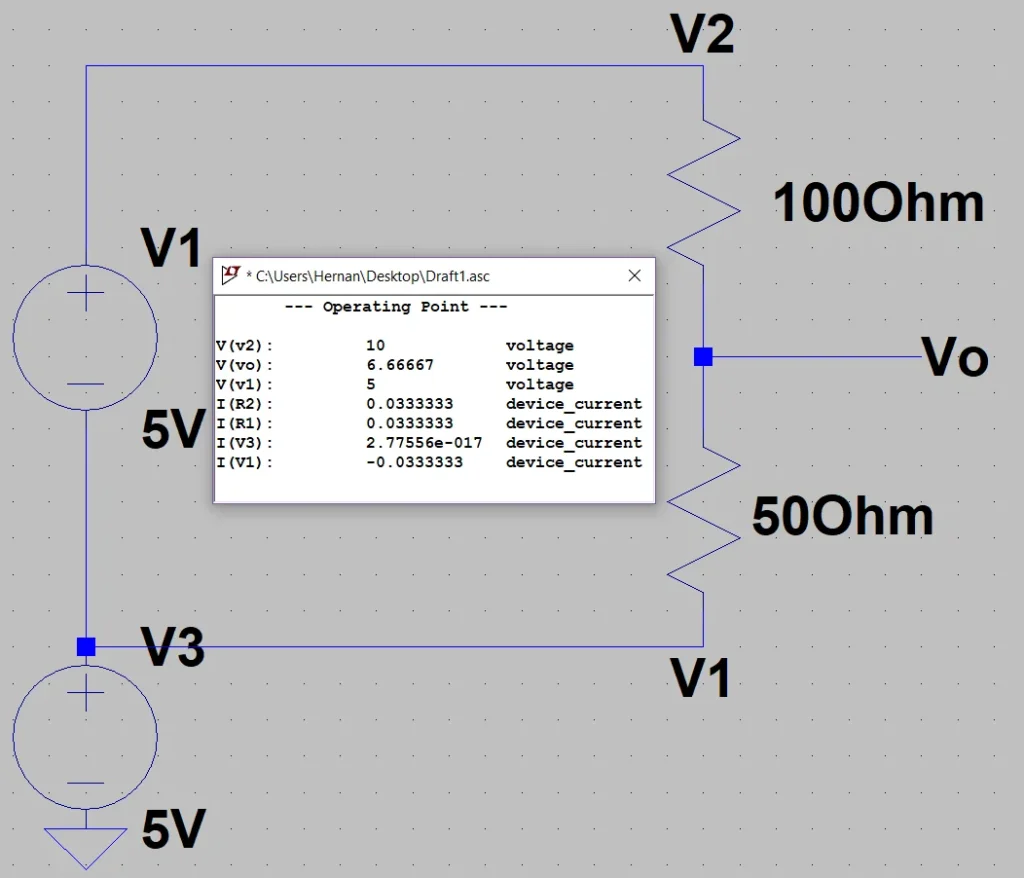
Análogamente a la figura 3, no debemos asumir que esto será siempre así, hay que recordar sumar la tensión aplicada en V1, esto podemos comprobarlo en las figuras 6 y 7.
Deducción de la fórmula
Ahora que hemos visto el principio de funcionamiento y algunos experimentos vamos a encontrar una expresión para el voltaje Vo que tenga en cuenta ambas resistencias.
El voltaje Vo va a ser igual al voltaje V1 más la caída de potencial en la resistencia 2.
Vo = V1 + Vr2
La caída de potencial en R2 es igual a la corriente que circula por la resistencia multiplicada por el valor de R2.
Vr2 = i x R2
Entonces:
Vo = V1 + i x R2
La corriente que circula por el divisor, por Ley de Ohm, es igual a la diferencia de potencial aplicada en los extremos dividido la suma de las resistencias.
i = ( V2 – V1 ) / ( R1 + R2 )
Reemplazando la corriente en la expresión anterior tenemos:
Vo = V1 + R2 x ( V2 – V1 ) / ( R1 + R2 )
Aquí ya tenemos una expresión para Vo en la que están todas las variables de la figura 1, sin embargo podemos resolver la suma y obtener una expresión más compacta.
Vo = ( R1 x V1 + R2 x V2) / ( R1 + R2 )
El Potenciómetro
Este elemento se puede usar como un divisor resistivo variable.
El potenciómetro básicamente son dos resistencias que podemos cambiar de valor pero la suma de ambas permanece invariable.
Si en los extremos conectamos una diferencia de potencial, en el medio tendremos un voltaje que estará entre el voltaje mínimo y el máximo de esa diferencia de potencial.
Utilizando la perilla podremos controlar el voltaje en la pata central.
Conclusión
Hemos visto qué es un divisor resistivo y cuál es su principio de funcionamiento.
Algunas aplicaciones pueden ser para ingresar valores en entradas analógicas de distintos aparatos de control como variadores de frecuencia o controladores lógicos. Polarizar transistores.
