The word "bit" comes from "bina­ry digit" 

Introduction — Numerical Systems

Before going into the main top­ic which is bit in com­put­er sci­ence, let's start from a math­e­mat­i­cal approach.

A dig­it is a quan­ti­ty of one fig­ure that has a val­ue and occu­pies a posi­tion in some numer­i­cal sys­tem. Let's take as an exam­ple the dec­i­mal sys­tem that we use on a dai­ly basis. This sys­tem is com­posed of 10 sym­bols that we call num­bers (0,1,2,3,4,5,6,7,8,9). Each of these sym­bols has a val­ue assigned to it and giv­en two dif­fer­ent num­bers we can order them for exam­ple from least to greatest.

It is also said that the dec­i­mal sys­tem is a "posi­tion­al sys­tem", that is to say that a dig­it acquires val­ue accord­ing to the posi­tion in which it is locat­ed. This is some­thing we are taught at a very ear­ly age, the sub­ject of "units", "tens" and "hun­dreds". The val­ues 1, 10 and 100 are com­posed of the same dig­it 1, but they are not worth the same because that dig­it is in dif­fer­ent posi­tions. In oth­er words the posi­tion in which a dig­it is found will have an asso­ci­at­ed weight, a 1 in third posi­tion is worth ten times more than a 1 in sec­ond posi­tion and one hun­dred times more than a 1 in first posi­tion.

Once a posi­tion­al num­ber sys­tem such as dec­i­mal has been estab­lished, we can begin to con­struct oper­a­tions between num­bers such as addi­tion, sub­trac­tion, mul­ti­pli­ca­tion and divi­sion.

Are there numer­i­cal sys­tems oth­er than decimal?

The use of the dec­i­mal sys­tem is cen­turies old and it is thought that its ori­gin lies in the fact that human beings are born with ten fin­gers. It is the numer­i­cal sys­tem that is most­ly used world­wide, how­ev­er noth­ing pre­vents us from using any num­ber of sym­bols to estab­lish a posi­tion­al numer­i­cal sys­tem, for exam­ple if instead of using 10 sym­bols we use 8 we have the octal numer­al sys­tem, on which the same math­e­mat­i­cal oper­a­tions of the dec­i­mal sys­tem are also defined.

Let's think about the fol­low­ing exam­ple, in the dec­i­mal sys­tem the oper­a­tion 9+1 gives as a result 10, where the 1 that is in the sec­ond posi­tion we know that it has a val­ue or weight of ten. If we take this same exam­ple to the octal sys­tem, in which we have the num­bers (0,1,2,3,4,5,6,7), the oper­a­tion 7+1 gives as a result 10, where the 1 in the sec­ond posi­tion has a val­ue or weight of eight.

Anoth­er known sys­tem is the hexa­dec­i­mal sys­tem that has 16 sym­bols (0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F), in this case the oper­a­tion F+1 results in 10, where the 1 in the sec­ond posi­tion has a val­ue of 16.

Anoth­er num­ber sys­tem can be the bina­ry sys­tem which is the one that inter­ests us in this arti­cle, the bina­ry sys­tem is com­posed of two sym­bols, zero and one, in this sys­tem the oper­a­tion 1+1 results in 10, in which the 1 that is in sec­ond posi­tion has a val­ue of 2. On the bina­ry sys­tem can also be per­formed the oper­a­tions of addi­tion, sub­trac­tion, mul­ti­pli­ca­tion and divi­sion, but it has also been devel­oped Boolean alge­bra that defines log­i­cal oper­a­tions between bina­ry num­bers as the oper­a­tions CONJUNCTION (AND) and DISJUNCTION (OR). And final­ly we come to the objec­tive of this arti­cle, reit­er­at­ing the open­ing sentence: 

A "BIT" is a dig­it of the bina­ry system.

What is a Bit in Computer Science?

In com­put­ing, the "bit" is the basic unit of infor­ma­tion, which allows us to dis­tin­guish between two states.

Bits are grouped togeth­er to form bina­ry words. A bina­ry word of 8 bits is known as a Byte and allows us to rep­re­sent 256 dif­fer­ent states.

The proces­sors in con­junc­tion with RAM and ROM per­form oper­a­tions using bina­ry words.

One way to under­stand how proces­sors work is to study the dif­fer­ent com­put­er archi­tec­tures. For more infor­ma­tion, see the Von Neu­mann archi­tec­ture.

So by using bytes (which are made up of bits) it is pos­si­ble to rep­re­sent increas­ing­ly com­plex infor­ma­tion, not only numer­i­cal, but also text, sounds, images, and to per­form log­i­cal and math­e­mat­i­cal oper­a­tions on that information.

For exam­ple, using 3 bytes we can rep­re­sent any col­or in the RGB sys­tem, one byte for the red chan­nel, one for the green chan­nel and one for the blue channel.

Anoth­er exam­ple could be that using a byte we can rep­re­sent a char­ac­ter, then a sen­tence will occu­py a space in mem­o­ry pro­por­tion­al to the num­ber of char­ac­ters that com­pose it.

What is the difference between BIT and BYTE?

Bit and Byte are two terms that are often con­fused or even used as syn­onyms, so let's empha­size this. As we saw ear­li­er, a BIT is a bina­ry dig­it that can have a val­ue of zero or one, while a BYTE is an ordered arrange­ment of EIGHT BITS. A bit allows us to rep­re­sent two dif­fer­ent states while a BYTE, being a com­bi­na­tion of EIGHT BITS allows us to rep­re­sent 256 dif­fer­ent states, 2 raised to the 8 pos­si­ble combinations.

The size of Information

I invite you to do a lit­tle exper­i­ment to see how much space infor­ma­tion takes up in com­put­ers. The exper­i­ment con­sists of open­ing Notepad and past­ing the fol­low­ing sen­tence with­out the quo­ta­tion marks:

"The let­ters that make up this phrase occu­py a cer­tain amount of mem­o­ry space." 

The pre­vi­ous phrase has 77 char­ac­ters, take a look of the size of the .txt file.

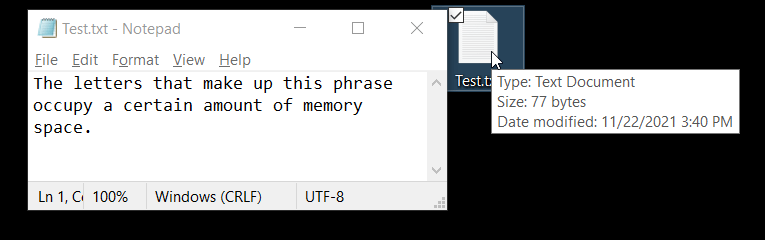
This is not always accu­rate because a text file does not store only char­ac­ters, but also infor­ma­tion about the for­mat to dis­play those char­ac­ters. In addi­tion, pro­grams can use com­pres­sion meth­ods to rep­re­sent the same infor­ma­tion in a more com­pact form, how­ev­er in the case of the notepad, the weight of the infor­ma­tion is usu­al­ly pro­por­tion­al to the num­ber of char­ac­ters, espe­cial­ly if there are only com­mon characters.

What is a Bit at the Hardware level?

It is said that com­put­ers work with ones and zeros, this is true at a the­o­ret­i­cal lev­el, but phys­i­cal­ly the bits are imple­ment­ed with volt­age lev­els, think of the lamp in a room that is turned on or off with a switch, when the switch is open, elec­tric­i­ty does not flow and the lamp is off, when the switch is closed, elec­tric­i­ty flows and the lamp is turned on, this exam­ple is sim­i­lar to what hap­pens inside the dig­i­tal microchips, where there are extreme­ly small switch­es (the size of dozens of atoms and every time they try to make them small­er) that open or close in a con­trolled man­ner, ie pre­vent the pas­sage of elec­tric­i­ty or allow it, in oth­er words at the out­put of that switch we can have a 0 or a 1. These small switch­es are called TRANSISTORS.

Micro­proces­sors are sys­tems made up of mil­lions of tran­sis­tors. Using tran­sis­tors it is pos­si­ble to cre­ate log­ic gates, from the most basic gate which is an INVERTER that imple­ments the log­i­cal oper­a­tion NOT, that is to say if the input is 0 the out­put will be 1, to more com­plex gates such as the XOR gate, that giv­en two input bits, the out­put will be 1 if and only if one of the inputs is 1. In addi­tion these log­ic gates are grouped in increas­ing­ly com­plex dig­i­tal sys­tems to form flip flops, coun­ters, adders, shift reg­is­ters or mem­o­ry blocks.

RAM is anoth­er exam­ple, a block of volatile mem­o­ry, which stores bits tem­porar­i­ly to assist the proces­sor with its tasks.

The hard disk stores bits in the form of mag­net­ic fields using the mag­net­ic hys­tere­sis prop­er­ty of some mate­ri­als, while sol­id state disks store infor­ma­tion in flash mem­o­ry blocks, with no mov­ing parts.

Conclusion

A bit is a bina­ry dig­it that can be worth 0 or 1, it is part of a numer­ic sys­tem anal­o­gous to the dec­i­mal sys­tem we use, the bina­ry sys­tem, in which instead of hav­ing 10 num­bers, we have two.

The bit is the basic unit of infor­ma­tion used in com­put­ing. By group­ing bits into bina­ry words, all kinds of data such as num­bers, text, images or sounds can be rep­re­sent­ed, i.e. infor­ma­tion can be digitized.

The bit is a con­cept that is applied at the soft­ware lev­el to ana­lyze the infor­ma­tion and log­i­cal oper­a­tions that are per­formed. In micro­proces­sors this trans­lates phys­i­cal­ly to volt­age lev­els or mag­ne­ti­za­tion in the case of mag­net­ic hard drives.